题目内容
今欲制作一个容器为V的无盖圆柱形的桶，底用铝板，侧壁用木板，已知每平方米铝板价钱是木板价钱的5倍，则怎样才能使材料费用最少？
考点：基本不等式在最值问题中的应用
专题：应用题,不等式的解法及应用
分析：先确定h=
，表示出W=2πha+πR2•5a=a（
+5πR2），再用导数法求最值，即可得出结论．
| V |
| πR2 |
| 2Y |
| R |
解答：
解：设桶的底面半径为R，桶高为h，材料费用为W，每平方米木板价钱为a，则V=πR2h，
∴h=
，
∴W=2πha+πR2•5a=a（
+5πR2），
∴V′=a（10πR-
）=0可得R=
，
函数在（0，
）上单调递减，在（
，+∞）上单调递增，
∴R=
时，函数取得极小值，也是最小值
此时h=
．
∴h=
| V |
| πR2 |
∴W=2πha+πR2•5a=a（
| 2Y |
| R |
∴V′=a（10πR-
| 2V |
| R2 |
| 3 |
| ||
函数在（0，
| 3 |
| ||
| 3 |
| ||
∴R=
| 3 |
| ||
此时h=
| 3 |
| ||
点评：本题考查利用数学知识解决实际问题，考查导数知识的运用，属于中档题．
练习册系列答案
相关题目
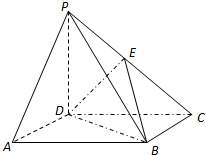如图所示，PD⊥底面ABCD，四边形ABCD是正方形，PD=DC，E是PC的中点．