题目内容
已知公差不为零的等差数列{an}中,a1=1,且a1,a3,a13成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=2an,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)设bn=2an,求数列{bn}的前n项和Sn.
考点:数列的求和,等差数列的通项公式,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)设等差数列{an}的公差为d,d≠0,由已知得(1+2d)2=1+12d,由此能求出an=2n-1.
(2)bn=2an=22n-1,数列{bn}是以2为首项,4为公比的等比数列.由此能求出Sn.
(2)bn=2an=22n-1,数列{bn}是以2为首项,4为公比的等比数列.由此能求出Sn.
解答:
解:(1)设等差数列{an}的公差为d,d≠0,
∵a1=1,且a1,a3,a13成等比数列,
∴a32=a1a13,
∴(1+2d)2=1+12d,解得d=2或d=0(舍),
∴an=2n-1.
(2)bn=2an=22n-1,
∴数列{bn}是以2为首项,4为公比的等比数列.
∴Sn=2+23+25+…+22n-1
=
=
(4n-1).
∵a1=1,且a1,a3,a13成等比数列,
∴a32=a1a13,
∴(1+2d)2=1+12d,解得d=2或d=0(舍),
∴an=2n-1.
(2)bn=2an=22n-1,
∴数列{bn}是以2为首项,4为公比的等比数列.
∴Sn=2+23+25+…+22n-1
=
| 2(1-4n) |
| 1-4 |
| 2 |
| 3 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示.问:
2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示.问: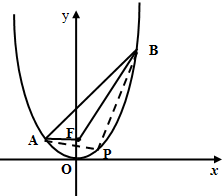 如图,已知抛物线x2=4y上两定点A,B分别在对称轴左、右两侧,F为抛物线的焦点,且|AF|=2,|BF|=5.
如图,已知抛物线x2=4y上两定点A,B分别在对称轴左、右两侧,F为抛物线的焦点,且|AF|=2,|BF|=5.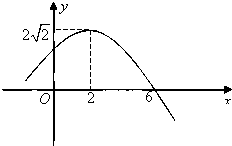 已知函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0,|φ|<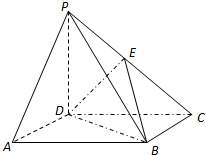 如图所示,PD⊥底面ABCD,四边形ABCD是正方形,PD=DC,E是PC的中点.
如图所示,PD⊥底面ABCD,四边形ABCD是正方形,PD=DC,E是PC的中点. 已知函数f(x)=ax3+bx2+cx在点x0处取得极小值,其导函数y=f'(x)的图象经过点(1,0),(2,0),如图所示.则x0=
已知函数f(x)=ax3+bx2+cx在点x0处取得极小值,其导函数y=f'(x)的图象经过点(1,0),(2,0),如图所示.则x0=