Question

12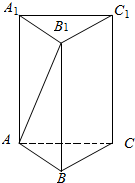．如图，在正三棱柱ABC-A₁B₁C₁中，若BB₁=$\sqrt{2}$，AB=2$\sqrt{2}$，求点C到直线AB₁的距离．

Answer 1

分析 利用几何体求出三角形CAB₁的三个边长，然后求解C到直线AB₁的距离．

解答 解：在正三棱柱ABC-A₁B₁C₁中，若BB₁=$\sqrt{2}$，AB=2$\sqrt{2}$，连结B₁C，
可得AB₁=$\sqrt{{（2\sqrt{2}）}^{2}+{（\sqrt{2}）}^{2}}$=$\sqrt{10}$，
B₁C$\sqrt{{（2\sqrt{2}）}^{2}+{（\sqrt{2}）}^{2}}$=$\sqrt{10}$
AC=2$\sqrt{2}$．作B₁F⊥AC于F，
B₁F=$\sqrt{（\sqrt{10}）^{2}-（\sqrt{2}）^{2}}$=$2\sqrt{2}$，
在三角形ACB₁中，CE⊥AB₁，CE就是点C到直线AB₁的距离：$\frac{AC•{B}_{1}F}{{AB}_{1}}$=$\frac{2\sqrt{2}×2\sqrt{2}}{\sqrt{10}}$=$\frac{4\sqrt{10}}{5}$．

点评 本题考查空间点线面距离的计算，考查计算能力空间想象能力．