题目内容
式子sin34°sin26°-cos34°cos26°的值为( )
A、
| ||
| B、cos8° | ||
C、-
| ||
| D、-cos8° |
考点:两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:可由两角和的余弦公式逆着运用,再由特殊角的三角函数值,即可得到所求值.
解答:
解:sin34°sin26°-cos34°cos26°
=-(cos34°cos26°-sin34°sin26°)
=-cos(34°+26°)
=-cos60°=-
.
故选C.
=-(cos34°cos26°-sin34°sin26°)
=-cos(34°+26°)
=-cos60°=-
| 1 |
| 2 |
故选C.
点评:本题考查逆用两角和的余弦公式,考查运算能力,属于基础题.

练习册系列答案
相关题目
如图,已知长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,则二面角B1-AC-B的余弦值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若
(2x-3x2)dx=0,则k=( )
| ∫ | k 0 |
| A、1 | B、0 |
| C、0或1 | D、以上都不对 |
数列{an}满足a1=1,_an=
(n≥2),则使得ak>
的最大正整数k为( )
| an-1 |
| an-1+2 |
| 1 |
| 2009 |
| A、5 | B、7 | C、8 | D、10 |
将1,2,3,4,5,6,7,8,这八个数分别填写于一个圆周的八等分点上,使得圆周上任意两个相邻位置的数之和为质数,如果圆周旋转后能重合的算作相同填法,那么不同的填法有( )
| A、4种 | B、8种 |
| C、12种 | D、16种 |
已知集合A={x∈R|0<x<1},B={x∈R|(2x-1)(x+1)≤0},则(∁RA)∩B( )
A、[0,
| ||
| B、[-1,0] | ||
C、[
| ||
| D、(-∞,-1]∪[0,+∞) |
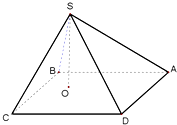 在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是( )
在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是( )