题目内容
已知集合A={x∈R|0<x<1},B={x∈R|(2x-1)(x+1)≤0},则(∁RA)∩B( )
A、[0,
| ||
| B、[-1,0] | ||
C、[
| ||
| D、(-∞,-1]∪[0,+∞) |
考点:交、并、补集的混合运算
专题:计算题,集合
分析:先求出集合B与∁RA,再求(∁RA)∩B.
解答:
解:B={x∈R|(2x-1)(x+1)≤0}={x|-1≤x≤
},
∁RA={x|x≤0或x≥1},
则(∁RA)∩B={x|-1≤x≤0}.
故选B.
| 1 |
| 2 |
∁RA={x|x≤0或x≥1},
则(∁RA)∩B={x|-1≤x≤0}.
故选B.
点评:本题考查了集合的运算,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
式子sin34°sin26°-cos34°cos26°的值为( )
A、
| ||
| B、cos8° | ||
C、-
| ||
| D、-cos8° |
 该茎叶图记录了甲、乙两组各五名学生在一次数学测试中的成绩(单位:分),已知甲组数据的平均数为87,乙组数据的中位数为87,则x,y的值分别为( )
该茎叶图记录了甲、乙两组各五名学生在一次数学测试中的成绩(单位:分),已知甲组数据的平均数为87,乙组数据的中位数为87,则x,y的值分别为( )| A、2,6 | B、2,7 |
| C、3,6 | D、3,7 |
函数y=e-x2+2x(0≤x<3)的值域是( )
| A、(e-3,1) |
| B、[e-3,1) |
| C、(e-3,e] |
| D、(1,e] |
(文)若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,有下面四个结论:
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等
③连接四面体ABCD每组对棱中点的线段互垂直平分;
④从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边
其中正确结论的个数有( )
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等
③连接四面体ABCD每组对棱中点的线段互垂直平分;
④从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边
其中正确结论的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
设定义在R上的函数f(x)=
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的实数解x1,x2,x3,则x1+x2+x3等于( )
|
| A、3 | B、6 | C、-b-1 | D、c |
函数f(x)=2lnx+2x-5的零点个数为( )
| A、1 | B、2 | C、0 | D、3 |
如图,D为等腰三角形ABC底边AB的中点,则下列等式恒成立的是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
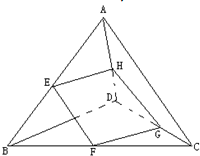 已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.
已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.