题目内容
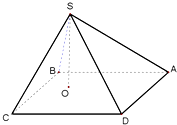在四棱锥S-ABCD中，底面ABCD是边长为a的正方形，顶点S在底面内的射影O在正方形ABCD的内部（不在边上），且SO=λa，λ为常数，设侧面SAB，SBC，SCD，SDA与底面ABCD所成的二面角依次为α1，α2，α3，α4，则下列各式为常数的是（ ）①
| 1 |
| tanα1 |
| 1 |
| tanα2 |
②
| 1 |
| tanα1 |
| 1 |
| tanα3 |
③
| 1 |
| tanα2 |
| 1 |
| tanα3 |
④
| 1 |
| tanα2 |
| 1 |
| tanα4 |
| A、①② | B、②④ | C、②③ | D、③④ |
考点：二面角的平面角及求法
专题：空间角
分析：过O点作MN⊥BC，根据二面角的定义易得∠SMO即为侧面SBC与底面ABCD所成的二面角，∠SNO即为侧面SDA与底面ABCD所成的二面角，根据余切函数的定义及SO=λa，λ为常数，易得到答案．
解答：
解：过O点作MN⊥BC，则BC⊥AD，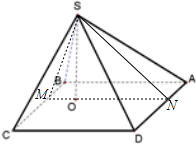
则OM，ON分别为BM，BN在底面ABCD上的射影
则∠SMO即为侧面SBC与底面ABCD所成的二面角，
∠SNO即为侧面SDA与底面ABCD所成的二面角，
∴∠SMO=α1，∠SNO=α3，
故
=
，
=
，
则
+
=
+
=
=
=
为定值
同理可得
+
为定值
故选：B．
则OM，ON分别为BM，BN在底面ABCD上的射影
则∠SMO即为侧面SBC与底面ABCD所成的二面角，
∠SNO即为侧面SDA与底面ABCD所成的二面角，
∴∠SMO=α1，∠SNO=α3，
故
| 1 |
| tanα1 |
| OM |
| OS |
| 1 |
| tanα3 |
| ON |
| OS |
则
| 1 |
| tanα1 |
| 1 |
| tanα2 |
| OM |
| OS |
| ON |
| OS |
| MN |
| OS |
| a |
| λa |
| 1 |
| λ |
同理可得
| 1 |
| tanα2 |
| 1 |
| tanα4 |
故选：B．
点评：本题以正切函数的定义为载体考查了二面角的定义，其中根据二面角的定义求出二面角的平面角是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
在平行四边形ABCD中，E、F分别是边CD和BC的中点，若
=λ
+μ
，其中λ、μ∈R，则λ+μ=（ ）
| AC |
| AE |
| AF |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
式子sin34°sin26°-cos34°cos26°的值为（ ）
A、
| ||
| B、cos8° | ||
C、-
| ||
| D、-cos8° |
已知平面上有A、B、C、D四点，这四点可确定的直线最多有（ ）
| A、4条 | B、6条 | C、8条 | D、10条 |
设a=log37，b=21.1，c=0.83.1，则（ ）
| A、b＜a＜c |
| B、c＜a＜b |
| C、c＜b＜a |
| D、a＜c＜b |