题目内容
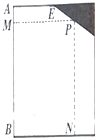如图，已知边长为16米的正方形钢板有一个角锈蚀，其中AE=8米，CD=12米，为了合理利用这块钢板，将五边形ABCDE内截取一个矩形块BNPM，使点P在边DE上，则矩形BNPM面积的最大值为考点：基本不等式在最值问题中的应用
专题：计算题,空间位置关系与距离
分析：设AM=x，由题可知，BM=16-x，MP=8+2x且0≤x≤4，设矩形面积为S，则S=（8+2x）（16-x），再根据二次函数的性质，求得S的最大值．
解答：
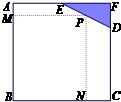解：设AM=x，由题可知，BM=16-x，MP=8+2x且0≤x≤4，
设矩形面积为S，则S=（8+2x）（16-x），
即S=-2x2+24x+128=-2（x-6）2+56．
当x∈（-∞，6]时S递增，而[0，4]⊆（-∞，6]，
∴当x=6时，S取最大值，Smax=56平方米．
故答案为：56．
解：设AM=x，由题可知，BM=16-x，MP=8+2x且0≤x≤4，设矩形面积为S，则S=（8+2x）（16-x），
即S=-2x2+24x+128=-2（x-6）2+56．
当x∈（-∞，6]时S递增，而[0，4]⊆（-∞，6]，
∴当x=6时，S取最大值，Smax=56平方米．
故答案为：56．
点评：本题考查函数解析式的确定，考查配方法求函数的最值，考查学生的计算能力，属于中档题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
正项等比数列{an}中，若log2（a1a9）=4，则a3a7等于（ ）
| A、16 | B、-16 |
| C、10 | D、256 |
设m，n，p，q是满足条件m+n=p+q的任意正整数，则对各项不为0的数列{an}，am•an=ap•aq是数列{an}为等比数列的（ ）条件．
| A、充分不必要 |
| B、必要不充分 |
| C、充要条件 |
| D、既不充分也不必要 |
已知函数f（x）（x∈R）满足f′（x）＞f（x），则（ ）
| A、f（1）＞ef（0）＞e2f（-1） |
| B、f（1）＜ef（0）＜e2f（-1） |
| C、e2f（-1）＞ef（0）＞f（1） |
| D、e2f（-1）＜ef（0）＜f（1） |