题目内容
已知函数f（x）（x∈R）满足f′（x）＞f（x），则（ ）
| A、f（1）＞ef（0）＞e2f（-1） |
| B、f（1）＜ef（0）＜e2f（-1） |
| C、e2f（-1）＞ef（0）＞f（1） |
| D、e2f（-1）＜ef（0）＜f（1） |
考点：导数的运算
专题：导数的综合应用
分析：根据条件，构造函数g（x）=
，利用函数的单调性研究函数值的大小，即可得到结论
| f(x) |
| ex-1 |
解答：
解：设g（x）=
，
则g′（x）=
=
，
由于函数f（x）（x∈R）满足f′（x）＞f（x），且ex-1＞0恒成立，
则g′（x）＞0，即函数g（x）为增函数，
由于-1＜0＜1，则g（-1）＜g（0）＜g（1）
即
＜
＜
，故f（1）＞ef（0）＞e2f（-1），
故选：A．
| f(x) |
| ex-1 |
则g′（x）=
| f′(x)ex-1-f(x)ex-1 |
| (ex-1)2 |
| f′(x)-f(x) |
| ex-1 |
由于函数f（x）（x∈R）满足f′（x）＞f（x），且ex-1＞0恒成立，
则g′（x）＞0，即函数g（x）为增函数，
由于-1＜0＜1，则g（-1）＜g（0）＜g（1）
即
| f(-1) |
| e-1-1 |
| f(0) |
| e0-1 |
| f(1) |
| e1-1 |
故选：A．
点评：本题考查了利用函数的导数研究函数的单调性基本方法，恰当构造函数是解题的关键．
练习册系列答案
相关题目
在等差数列{an}中，若a2=1，a8=2a6+a4，则a5的值是（ ）
| A、-5 | ||
B、-
| ||
C、
| ||
D、
|
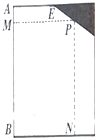如图，已知边长为16米的正方形钢板有一个角锈蚀，其中AE=8米，CD=12米，为了合理利用这块钢板，将五边形ABCDE内截取一个矩形块BNPM，使点P在边DE上，则矩形BNPM面积的最大值为
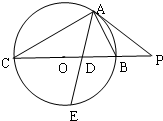如图，△ABC内接于直径为F1，F2的圆P，过点A作圆O的切线交CB的延长线于点P，∠BAC的平分线分别交BC和圆O于点D、E，若PA=2PB=10