题目内容

已知8sinα+5cosβ=6，sin（α+β）=
47
80
，则8cosα+5sinβ=
 
．
考点：两角和与差的正弦函数,两角和与差的余弦函数
专题：三角函数的求值
分析：设8cosα+5sinβ=t，①，8sinα+5cosβ=6，②，两式平方相加代值计算可得．
解答： 解：设8cosα+5sinβ=t，①
∵8sinα+5cosβ=6，②
①②两式平方相加可得8+5+80（cosαsinβ+sinαcosβ）=t2+36，
∴13+80sin（α+β）=t2+36，
∴t2=80×
47
80
-23=24，
∴8cosα+5sinβ=t=±2
6

故答案为：±2
6
点评：本题考查两角和与差的正余弦函数，平方相加是解决问题的关键，属基础题．
练习册系列答案
相关题目
如图所示，现有一迷失方向的小青蛙在3处，它每跳动一次可以等可能地进入相邻的任意一格（若它在5处，跳动一次，只能进入3处，若在3处，则跳动一次可以等机会进入1，2，4，5处），则它在第三次跳动后，首次进入5处的概率是（　　）
A、
3
16
B、
1
4
C、
1
6
D、
1
2
调查表明，中年人的成就感与收入、学历、职业的满意度的指标有极强的相关性．现
将这三项的满意度指标分别记为x，y，z，并对它们进行量化：0表示不满意，1表示基本满意，2表示满意，再用综合指标w=x+y+z的值评定中年人的成就感等级：若w≥4，则成就感为一级；若2≤w≤3，则成就感为二级；若0≤w≤1，则成就感为三级．为了了解目前某群体中年人的成就感情况，研究人员随机采访了该群体的10名中年人，得到如下结果：
人员编号A1A2A3A4A5
（x，y，z）（1，1，2）（2，1，1）（2，2，2）（0，1，1）（1，2，1）
人员编号A6A7A8A9A10
（x，y，z）（1，2，2）（1，1，1）（1，2，2）（1，0，0）（1，1，1）
（Ⅰ）在这10名被采访者中任取两人，求这两人的职业满意度指标相同的概率；
（Ⅱ）从成就感等级是一级的被采访者中任取一人，其综合指标为a，从成就感等级不是一级的被采访者中任取一人，其综合指标为b，记随机变量X=a-b，求X的分布列及其数学期望．
要从5名女生，7名男生中选出5名代表，按下列要求，分别有多少中不同的选法？
（1）有2名女生入选；
（2）至少有1名女生入选；
（3）至多有2名女生入选；
（4）女生甲必须入选；
（5）男生A不能入选；
（6）女生甲、乙两人恰有1人入选．
在△ABC中，角A，B，C所对的边长分别为a，b，c，tanA=
1
4
，tanB=
3
5
，
（1）求角C的大小；
（2）若△ABC中最长的边为
17
，求最短边的长．
已知等差数列{an}的前n项和为377，项数n为奇数，且前n项和中奇数项和与偶数项和之比为7：6，求中间项．
等差数列{an}中，a7+a14=80，求前20项之和S20．
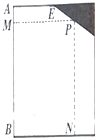如图，已知边长为16米的正方形钢板有一个角锈蚀，其中AE=8米，CD=12米，为了合理利用这块钢板，将五边形ABCDE内截取一个矩形块BNPM，使点P在边DE上，则矩形BNPM面积的最大值为
 
平方米．
i为虚数单位，若
.
z
=
1+7i
1-i
，则z等于（　　）
A、-3+4iB、3+4i
C、-3-4iD、3-4i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网