题目内容
设m,n,p,q是满足条件m+n=p+q的任意正整数,则对各项不为0的数列{an},am•an=ap•aq是数列{an}为等比数列的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要条件 |
| D、既不充分也不必要 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据等比数列的性质以及充分条件和必要条件的定义进行判断即可.
解答:
解:若数列{an}为等比数列,则对任意任意正整数m,n,p,q,若m+n=p+q,恒有am•an=ap•aq成立,
若a1=2,a4=4,a3=4,a2=2,
满足a1•a4=a3•a2,但数列{an}为{2,2,4,4}不是等比数列,
故am•an=ap•aq是数列{an}为等比数列的必要不充分条件,
故选:B.
若a1=2,a4=4,a3=4,a2=2,
满足a1•a4=a3•a2,但数列{an}为{2,2,4,4}不是等比数列,
故am•an=ap•aq是数列{an}为等比数列的必要不充分条件,
故选:B.
点评:本题主要考查充分条件和必要条件的判断,根据等比数列的性质是解决本题的关键.

练习册系列答案
相关题目
定义运算a?b为执行如图所示的程序框图输出的S值,则(2cos
)?tan
的值为( )
| π |
| 3 |
| 7π |
| 4 |

| A、2 | B、-2 | C、-1 | D、1 |
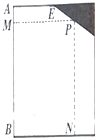 如图,已知边长为16米的正方形钢板有一个角锈蚀,其中AE=8米,CD=12米,为了合理利用这块钢板,将五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上,则矩形BNPM面积的最大值为
如图,已知边长为16米的正方形钢板有一个角锈蚀,其中AE=8米,CD=12米,为了合理利用这块钢板,将五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上,则矩形BNPM面积的最大值为已知全集U=R,集合M={x|-2≤x<2},P={x|y=
},则M∩(∁UP)等于( )
| x |
| A、[-2,0) |
| B、[-2,0] |
| C、[0,2) |
| D、(0,2) |
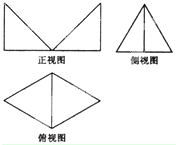 某几何体的三视图如图所示,某正视图是两个全等的三角形,俯视图是一个边长为2的正三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为
某几何体的三视图如图所示,某正视图是两个全等的三角形,俯视图是一个边长为2的正三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为