题目内容
已知函数f(x)=lnx,g(x)=
x2+mx+
(m<0),直线l与函数f(x)、g(x)的图象都相切,且与函数f(x)的图象的切点的横坐标为1.
(1)求直线l的方程及实数m的值;
(2)若函数h(x)=f(x)-g′(x)(其中g′(x)是g(x)′的导函数),求函数h(x)的最大值;
(3)当0<b<a时,求证:alna+blnb>(a+b)ln
.
| 1 |
| 2 |
| 7 |
| 2 |
(1)求直线l的方程及实数m的值;
(2)若函数h(x)=f(x)-g′(x)(其中g′(x)是g(x)′的导函数),求函数h(x)的最大值;
(3)当0<b<a时,求证:alna+blnb>(a+b)ln
| a+b |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)根据导数的几何意义,建立方程关系即可求直线l的方程及实数m的值;
(2)根据函数的最值和导数之间的关系,即可求函数h(x)的最大值;
(3)将不等式进行等价变形,利用凸凹函数的性质进行判断.
(2)根据函数的最值和导数之间的关系,即可求函数h(x)的最大值;
(3)将不等式进行等价变形,利用凸凹函数的性质进行判断.
解答:
解:(Ⅰ)∵直线l与函数f(x)的图象相切,且切点的横坐标为1.
∴切点坐标为P(1,ln1),即P(1,0)
∴f′(x)=
,即切线斜率为k=f′(1)=1,
∴直线l的方程为y=x-1
又∵直线l与函数y=g(x)的图象相切,设切点为Q(x0,x0-1)
∴
,
解得m=-2或4
∵m<0,∴x0=-2
故所求直线方程为y=x-1,m的值是-2.
(Ⅱ)由(I)得g′(x)=x-2
∴h(x)=f(x)-g′(x)=lnx-x+2
求导:h′(x)=
-1=
,x>0,
由h'(x)>0得0<x<1,此时函数单调递增,
由h'(x)<0得x>1,此时函数单调递减,
∴当x=1时,函数f(x)取得极大值,同时也是最大值,h(1)=ln1-1+2=1.
(Ⅲ)构造函数f(x)=xlnx+(4-x)ln(4-x),
∴f′(x)=lnx-ln(4-x)=ln
.
∴当x=2时,函数f(x)有最小值.a>0,b>0,
不妨设a+b=4,
则alna+blnb=alna+(4-a)ln(4-a)≥2•
ln(
)=(a+b)ln
,
∴alna+blnb≥(a+b)ln
,
∵0<b<a,∴等号取不到,
故alna+blnb>(a+b)ln
成立.
∴切点坐标为P(1,ln1),即P(1,0)
∴f′(x)=
| 1 |
| x |
∴直线l的方程为y=x-1
又∵直线l与函数y=g(x)的图象相切,设切点为Q(x0,x0-1)
∴
|
解得m=-2或4

∵m<0,∴x0=-2
故所求直线方程为y=x-1,m的值是-2.
(Ⅱ)由(I)得g′(x)=x-2
∴h(x)=f(x)-g′(x)=lnx-x+2
求导:h′(x)=
| 1 |
| x |
| 1-x |
| x |
由h'(x)>0得0<x<1,此时函数单调递增,
由h'(x)<0得x>1,此时函数单调递减,
∴当x=1时,函数f(x)取得极大值,同时也是最大值,h(1)=ln1-1+2=1.
(Ⅲ)构造函数f(x)=xlnx+(4-x)ln(4-x),
∴f′(x)=lnx-ln(4-x)=ln
| x |
| 4-x |
∴当x=2时,函数f(x)有最小值.a>0,b>0,
不妨设a+b=4,
则alna+blnb=alna+(4-a)ln(4-a)≥2•
| a+b |
| 2 |
| a+b |
| 2 |
| a+b |
| 2 |
∴alna+blnb≥(a+b)ln
| a+b |
| 2 |
∵0<b<a,∴等号取不到,
故alna+blnb>(a+b)ln
| a+b |
| 2 |
点评:本题主要考查导数的应用,利用函数单调性,极值和最值与导数之间的关系是解决本题的关键,综合性较强,运算量较大.

练习册系列答案
相关题目
“p∨q是真命题”是“?p为假命题”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
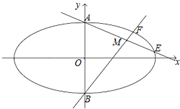 已知椭圆Γ:
已知椭圆Γ: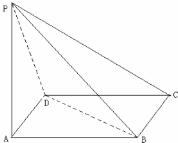 四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=
四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=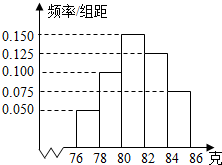 某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是
某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是