题目内容
已知等差数列{an}中,a2=4;a4是a2与a8的等比中项.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若an+1≠an.求数列{2n-1an}的前n项和.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若an+1≠an.求数列{2n-1an}的前n项和.
考点:数列的求和,等比数列的通项公式
专题:计算题,等差数列与等比数列
分析:(Ⅰ)依题意,可求得该等差数列的公差d=0或d=2,分类讨论,即可得到数列{an}的通项公式;
(Ⅱ)易求an=2n,2n-1an=2n-1•2n=2n•n,Sn=1×21+2×22+…+(n-1)•2n-1+n•2n,利用错位相减法即可求得Sn.
(Ⅱ)易求an=2n,2n-1an=2n-1•2n=2n•n,Sn=1×21+2×22+…+(n-1)•2n-1+n•2n,利用错位相减法即可求得Sn.
解答:
解:(Ⅰ)∵a2=4,a4是a2与a8的等比中项,
∴a1+d=4,a42=a2•a8,
即(4+2d)2=4(4+6d),化简得d2-2d=0,
解得:d=0或d=2;
由于a2=4,
∴当d=0时,an=4,
当d=2时,a1=2,an=2n;
(Ⅱ)∵an+1≠an,
∴an=2n,
∴2n-1an=2n-1•2n=2n•n,
∵Sn=1×21+2×22+…+(n-1)•2n-1+n•2n,①
∴2Sn=1×22+2×23+…+(n-1)•2n+n•2n+1,②
①-②得:
-Sn=21+22+…+2n-1+2n-n•2n+1
=
-n•2n+1
=(1-n)2n+1-2,
∴Sn=(n-1)•2n+1+2.
∴a1+d=4,a42=a2•a8,
即(4+2d)2=4(4+6d),化简得d2-2d=0,
解得:d=0或d=2;
由于a2=4,
∴当d=0时,an=4,
当d=2时,a1=2,an=2n;
(Ⅱ)∵an+1≠an,
∴an=2n,
∴2n-1an=2n-1•2n=2n•n,
∵Sn=1×21+2×22+…+(n-1)•2n-1+n•2n,①
∴2Sn=1×22+2×23+…+(n-1)•2n+n•2n+1,②
①-②得:
-Sn=21+22+…+2n-1+2n-n•2n+1
=
| 2(1-2n) |
| 1-2 |
=(1-n)2n+1-2,
∴Sn=(n-1)•2n+1+2.
点评:本题考查数列的求和,着重考查等差数列的通项公式与错位相减法求和,考查运算求解能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而甲、丁两机不能相邻着舰,那么不同的着舰方法有( )
| A、12种 | B、16种 |
| C、24种 | D、36种 |
若
,
是夹角为60°的单位向量,则
=2
+
,
=3
+2
的夹角为( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
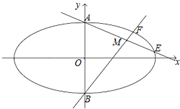 已知椭圆Γ:
已知椭圆Γ: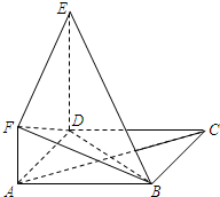 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2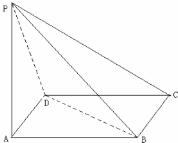 四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=
四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=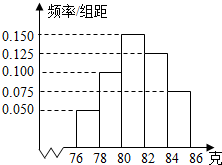 某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是
某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是