题目内容
函数f(x)=log2
,等比数列{an}中,a2•a5•a8=8,则f(a1)+f(a2)+…+f(a9)= .
| x |
| 4 |
考点:等比数列的性质
专题:函数的性质及应用,等差数列与等比数列
分析:根据等比数列的性质求出a5=2,然后根据对数的运算法则进行化简计算即可得到结论.
解答:
解:等比数列{an}中,a2•a5•a8=8,
∴(a5)3=8,即a5=2,
∵函数f(x)=log2
=log2x-2,
∴f(a1)+f(a2)+…+f(a9)=(log?2a1+…+log?2a9)-2×9
=log?2(a1a2…a9)-18=log?2(a5)9-18=9log?22-18=9-18=-9,
故答案为:-9.
∴(a5)3=8,即a5=2,
∵函数f(x)=log2
| x |
| 4 |
∴f(a1)+f(a2)+…+f(a9)=(log?2a1+…+log?2a9)-2×9
=log?2(a1a2…a9)-18=log?2(a5)9-18=9log?22-18=9-18=-9,
故答案为:-9.
点评:本题主要考查等比数列的性质以及对数的运算法则,要求熟练掌握相应的运算公式和性质.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
以下四个命题中,真命题的个数是( )
①“若x+y=0,则x,y互为相反数”的逆命题;
②“若a>b,则a2>b2”的逆否命题;
③“若x=-3,则x2+x-6=0”的否命题;
④“若a+b是无理数,则a,b定为无理数”的逆命题.
①“若x+y=0,则x,y互为相反数”的逆命题;
②“若a>b,则a2>b2”的逆否命题;
③“若x=-3,则x2+x-6=0”的否命题;
④“若a+b是无理数,则a,b定为无理数”的逆命题.
| A、0 | B、1 | C、2 | D、3 |
某几何体的三视图如图所示,则该几何体的体积为( )


A、4
| ||||
B、
| ||||
C、
| ||||
| D、3 |
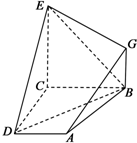 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=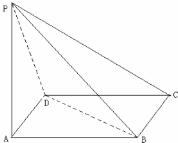 四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=
四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=