题目内容
已知双曲线C:
-y2=1(m>0),A.B两点分别在双曲线C的两条渐近线上,且|AB|=2
,又点P为AB的中点.
(1)求点P的轨迹方程并判断其形状;
(2)若不同三点D(-2,0)、S、T 均在点P的轨迹上,且
•
=0; 求T点横坐标xT的取值范围.
| x2 |
| m |
| m |
(1)求点P的轨迹方程并判断其形状;
(2)若不同三点D(-2,0)、S、T 均在点P的轨迹上,且
| DS |
| ST |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设出A,B的坐标,利用点P为AB的中点,确定坐标之间的关系,根据|AB|=2
,建立方程,化简,即可求点P的轨迹方程.
(2)直线DS、ST分别代入椭圆方程,求出T点横坐标,利用基本不等式,即可求T点横坐标xT的取值范围.
| m |
(2)直线DS、ST分别代入椭圆方程,求出T点横坐标,利用基本不等式,即可求T点横坐标xT的取值范围.
解答:
解:(1)双曲线渐近线为y=
与y=-
.
所以设A(xA,
),B(xB,-
),
所以xP=
,yP=
,
又|AB|=2
,
所以点P的轨迹方程为
+y2=1,
所以m=1时P的轨迹为圆;m>1时P的轨迹为焦点在x轴上的椭圆;0<m<1时P的轨迹为焦点在y轴上的椭圆;(6分)
(2)把D(-2,0)代入
+y2=1,得P的轨迹的
+y2=1…①
设直线DS为y=k(x+2)…②
联立①②得(1+4k2)x2+16k2x+16k2-4=0
设点S(x1,y1),有xD+x1=
,
所以x1=
,y1=
则直线ST为y=-
(x-x1)+y1
化简为:y=-
+
③
联立①,③得(1+
)x2+
x+
-4=0,
所以x1+xT=
,
所以xT=
-
=
=2-
( 因为三点不同,易知k≠0)
=2-
=
≥2-
=
所以xT的取值范围为[
,2)…(14分)
| x | ||
|
| x | ||
|
所以设A(xA,
| xA | ||
|
| xB | ||
|
所以xP=
| xA+xB |
| 2 |
| xA-xB | ||
2
|
又|AB|=2
| m |
所以点P的轨迹方程为
| x2 |
| m2 |
所以m=1时P的轨迹为圆;m>1时P的轨迹为焦点在x轴上的椭圆;0<m<1时P的轨迹为焦点在y轴上的椭圆;(6分)
(2)把D(-2,0)代入
| x2 |
| m2 |
| x2 |
| 4 |
设直线DS为y=k(x+2)…②
联立①②得(1+4k2)x2+16k2x+16k2-4=0
设点S(x1,y1),有xD+x1=
| -16k2 |
| 1+4k2 |
所以x1=
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
则直线ST为y=-
| 1 |
| k |
化简为:y=-
| x |
| k |
| 2-4k2 |
| k(1+4k2) |
联立①,③得(1+
| 4 |
| k2 |
| 32k2-16 |
| k2(1+4k2) |
| 4(2-4k2)2 |
| k2(1+4k2)2 |
所以x1+xT=
| 16-32k2 |
| (4+k2)(1+4k2) |
所以xT=
| 16-32k2 |
| (4+k2)(1+4k2) |
| 2-8k2 |
| 1+4k2 |
| 8k4-2k2+8 |
| 4k4+17k2+4 |
| 36k2 |
| 4k4+17k2+4 |
=2-
| 36k2 |
| 4k4+17k2+4 |
| 36 | ||
4(k2+
|
| 36 |
| 25 |
| 14 |
| 25 |
所以xT的取值范围为[
| 14 |
| 25 |
点评:本题考查轨迹方程,考查代入法的运用,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,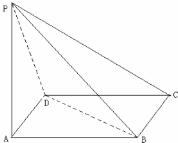 四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=
四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=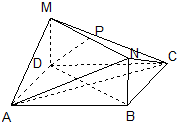 在如图所示的几何体中,四边形ABCD和BDMN都是矩形,且MD⊥平面ABCD,P是MN的中点.若AB=4,BC=3,MD=1,
在如图所示的几何体中,四边形ABCD和BDMN都是矩形,且MD⊥平面ABCD,P是MN的中点.若AB=4,BC=3,MD=1,