题目内容
20.F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的右焦点,点P在双曲线右支上,△POF(O为坐标原点)满足OF=OP=5,$P{F_{\;}}=2\sqrt{5}$,则双曲线的离心率为 ( )| A. | $\sqrt{3}+1$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 运用余弦定理可得cos∠OFP,求得sin∠OFP,求得P的坐标,代入双曲线方程,结合a,b,c的关系,求得a,再由离心率公式,计算即可得到.
解答 解:由余弦定理可得cos∠OFP=$\frac{{5}^{2}+{5}^{2}-(2\sqrt{5})^{2}}{2×5×5}$=$\frac{3}{5}$,
则sin∠OFP=$\sqrt{1-co{s}^{2}∠OFP}$=$\frac{4}{5}$,
可设P为第一象限的点,
即有P(3,4),
代入双曲线方程,可得$\frac{9}{{a}^{2}}-\frac{16}{{b}^{2}}=1$,
又a2+b2=25,
解得a=$\sqrt{5}$,b=2$\sqrt{5}$,
则离心率为e=$\sqrt{5}$.
故选:B.
点评 本题考查双曲线的方程和性质,主要考查双曲线的离心率的求法,同时考查余弦定理和任意角的三角函数的定义,考查运算能力,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
9.已知三棱锥S-ABC的所有顶点都在球O的球面上,球O的表面积为16π,△ABC是边长为3的正三角形,若SC⊥AB,SA⊥BC,则三棱锥S-ABC的体积的最大值为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{9\sqrt{3}}{4}$ | D. | $\frac{27\sqrt{3}}{4}$ |
10.已知双曲线C:$\frac{x^2}{16}-\frac{y^2}{b^2}=1({b>0})$的右焦点与抛物线y2=20x的焦点重合,则双曲线C的渐近线方程为( )
| A. | 4x±3y=0 | B. | 3x±4y=0 | C. | 16x±9y=0 | D. | 9x±16y=0 |
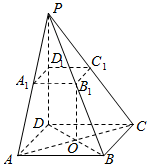 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.