题目内容
4.(1)计算:($\root{3}{3}$×$\sqrt{2}$)6+($\sqrt{3\sqrt{3}}$)${\;}^{\frac{4}{3}}$-$\root{4}{2}$×80.25-(-2019)0(2)已知0<x<1,且x+x-1=3,求x${\;}^{\frac{1}{2}}$-x${\;}^{-\frac{1}{2}}$.
分析 (1)利用有理数指数幂的性质、运算法则求解.
(2)利用有理数指数幂的性质、运算法则求解.
解答 解:(1)($\root{3}{3}$×$\sqrt{2}$)6+($\sqrt{3\sqrt{3}}$)${\;}^{\frac{4}{3}}$-$\root{4}{2}$×80.25-(-2019)0
=9×8+(${3}^{\frac{3}{4}}$)${\;}^{\frac{4}{3}}$-$1{6}^{\frac{1}{4}}$-1
=72+3-2-1
=72.
(2)∵0<x<1,且x+x-1=3,
∴(x${\;}^{\frac{1}{2}}$-x${\;}^{-\frac{1}{2}}$)2=x+x-1-2=1,
∵${x}^{\frac{1}{2}}<{x}^{-\frac{1}{2}}$,
∴${x}^{\frac{1}{2}}-{x}^{-\frac{1}{2}}$=-1.
点评 本题考查指数式化简求值,是基础题,解题时要认真审题,注意有理数指数幂的性质、运算法则的合理运用.

练习册系列答案
相关题目
12.设角α的终边经过点P(sin2,cos2),则$\sqrt{2(1-sinα)}$的值等于( )
| A. | sin1 | B. | cos1 | C. | 2sin1 | D. | 2cos1 |
19.对于使不等式f(x)≤M成立的所有常数M中,我们把M的最小值叫做函数f(x)的上确界.若a,b∈R+,a+b=1,则$-\frac{1}{2a}-\frac{2}{b}$的上确界为( )
| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{1}{4}$ | D. | -4 |
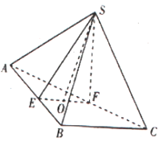 如图,三棱锥S-ABC,E,F分别在线段AB,AC上,EF∥BC,△ABC,△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.
如图,三棱锥S-ABC,E,F分别在线段AB,AC上,EF∥BC,△ABC,△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.