题目内容
13.在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知直线C1:$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),圆C2:$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数).(Ⅰ)当α=$\frac{π}{3}$时,求C1被C2截得的线段的长;
(Ⅱ)过坐标原点O作C1的垂线,垂足为A,当α变化时,求A点轨迹的极坐标方程.
分析 (Ⅰ)当α=$\frac{π}{3}$时,C1的普通方程为y=$\sqrt{3}$(x-1),C2的普通方程为x2+y2=1,联立方程组,解得C1与C2的交点,即可求C1被C2截得的线段的长;
(Ⅱ)求出A点坐标为(sin2α,-cosαsinα),可得普通方程,即可求A点轨迹的极坐标方程.
解答 解:(Ⅰ)当α=$\frac{π}{3}$时,C1的普通方程为y=$\sqrt{3}$(x-1),C2的普通方程为x2+y2=1.
联立方程组,解得C1与C2的交点为(1,0)与($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
所以,C1被C2截得的线段的长为1. …(5分)
(Ⅱ)将C1的参数方程代入C2的普通方程得t2+2tcosα=0,
∴A点对应的参数-cosα,∴A点坐标为(sin2α,-cosαsinα).
故A点轨迹的普通方程为(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$.
化为极坐标方程得ρ=cosθ. …(10分)
点评 本题考查三种方程的互化,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
1.已知等差数列{an}的前n项和为Sn,且S4=6,2a3-a2=6,则a1等于( )
| A. | -3 | B. | -2 | C. | 0 | D. | 1 |
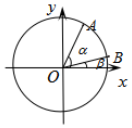 如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$
如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$