题目内容
9.已知函数f(x)=$\frac{2}{{{2^x}+1}}$+sinx,则f(-8)+f(-7)+f(-6)+…+f(8)=( )| A. | 0 | B. | 7 | C. | 17 | D. | 27 |
分析 推导出f(-x)+f(x)=2.由此能求出f(-8)+f(-7)+f(-6)+…+f(8)的值.
解答 解:∵函数f(x)=$\frac{2}{{{2^x}+1}}$+sinx,
∴f(-x)+f(x)=$\frac{2}{{2}^{-x}+1}+sin(-x)+\frac{2}{{2}^{x}+1}+sinx$
=$\frac{2•{2}^{x}}{1+{2}^{x}}-sinx+\frac{2}{{2}^{x}+1}+sinx$=2.
∴f(-8)+f(-7)+f(-6)+…+f(8)
=8×2+f(0)=16+$\frac{2}{{2}^{0}+1}$=17.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若曲线C1:y=x2与曲线C2:y=aex(a>0)至少存在两个交点,则a的取值范围为( )
| A. | [$\frac{8}{{e}^{2}}$,+∞) | B. | (0,$\frac{8}{{e}^{2}}$] | C. | [$\frac{4}{{e}^{2}}$,+∞) | D. | (0,$\frac{4}{{e}^{2}}$] |
1.已知等差数列{an}的前n项和为Sn,且S4=6,2a3-a2=6,则a1等于( )
| A. | -3 | B. | -2 | C. | 0 | D. | 1 |
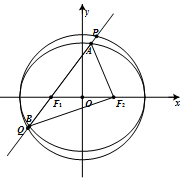 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=a2,F1(-1,0),F2(1,0)分别是椭圆的左、右两焦点,过F1且倾斜角为α$({α∈({0,\frac{π}{2}}]})$的动直线l交椭圆C于A,B两点,交圆O于P,Q两点(如图所示,点A在x轴上方).当α=$\frac{π}{4}$时,弦PQ的长为$\sqrt{14}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=a2,F1(-1,0),F2(1,0)分别是椭圆的左、右两焦点,过F1且倾斜角为α$({α∈({0,\frac{π}{2}}]})$的动直线l交椭圆C于A,B两点,交圆O于P,Q两点(如图所示,点A在x轴上方).当α=$\frac{π}{4}$时,弦PQ的长为$\sqrt{14}$. 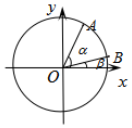 如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$
如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$