题目内容

1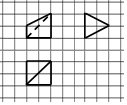．如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为（　　）
A．8πB．$\frac{25}{2}$πC．12πD．$\frac{41}{4}$π

分析 根据三视图得出空间几何体是镶嵌在正方体中的四棱锥O-ABCD，正方体的棱长为2，A，D为棱的中点，利用球的几何性质求解即可．

解答 解：根据三视图得出：该几何体是镶嵌在正方体中的四棱锥O-ABCD，正方体的棱长为2，A，D为棱的中点
根据几何体可以判断：球心应该在过A，D的平行于底面的中截面上，
设球心到截面BCO的距离为x，则到AD的距离为：2-x，
∴R2=x2+（$\sqrt{2}$）2，R2=12+（2-x）2，
解得出：x=$\frac{3}{4}$，R=$\frac{\sqrt{41}}{4}$，
该多面体外接球的表面积为：4πR2=$\frac{41}{4}$π，
故选D．

点评 本题综合考查了空间几何体的性质，学生的空间思维能力，构造思想，关键是镶嵌在常见的几何体中解决．

练习册系列答案
相关题目
2．下列关系正确的是（　　）
A．0=∅B．1∈{1}C．∅={0}D．0⊆{0，1}
3．如图1是遂宁市某校高中学生身高的条形统计图，从左到右的各条形表示的学生人数依次记为A1，A2，…，A10（如A2表示身高（单位：cm）[150，155）内的学生人数）．图2是图1中身高在一定分为内学生人数的一个算法流程图．现要统计身高在160～175cm（含160cm，不含175cm）的学生人数，那么在流程图中的判断框内应填入的条件是（　　）
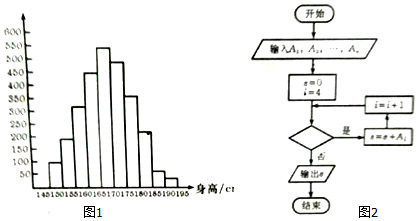
A．i＜6B．i＜7C．i＜8D．i＜9
20．数列$-\frac{1}{3}$，$\frac{1}{9}$，-$\frac{1}{27}$，$\frac{1}{81}$，…的一个通项公式可能是（　　）
A．（-1）n-1$\frac{1}{{3}^{n}}$B．（-1）n-1$\frac{1}{3n}$C．（-1）n$\frac{1}{{3}^{n}}$D．（-1）n$\frac{1}{3n}$
7．已知△ABC满足∠BAC=60°，BC=2，对于△ABC外接圆上一点D，满足∠BCD=45°，则BD=（　　）
A．$\sqrt{6}$B．$\sqrt{3}$C．$\frac{2\sqrt{3}}{3}$D．$\frac{2\sqrt{6}}{3}$
6．若$\sqrt{2}$sin（$\frac{π}{4}$-θ）+2=4cos2（$\frac{π}{4}$-$\frac{θ}{2}$），则tanθ=$\frac{1}{3}$．
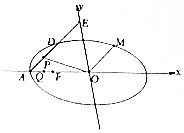13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1（a＞2$\sqrt{3}$）的左焦点为F，左顶点为A，$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$，其中O为原点，e为椭圆的离心率，过点A作斜率为k（k≠0）的直线l交椭圆C于点D，交y轴于点E．
（1）求椭圆C的方程；
（2）已知点Q（-3，0），P为线段AD上一点且|AP|=λ|AD|，是否存在定值λ使得OP⊥EQ恒成立，若存在，求出λ的值；若不存在，请说明理由．
10．已知过点A（-4，0）作动直线m与抛物线G：x2=2py（p＞0）相交于B、C两点．
（1）当直线的斜率是$\frac{1}{2}$时，$\overrightarrow{AC}$=4$\overrightarrow{AB}$，求抛物线G的方程；
（2）设B、C的中点是M，利用（1）中所求抛物线，试求点M的轨迹方程．
11．“直线ax+3y+3=0和直线4x+（a+1）y+4=0平行”的充要条件是“a=（　　）”
A．-4或3B．-$\frac{3}{7}$C．-3D．-4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网