题目内容
在四棱锥P ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a.点E为侧棱PC的中点,又作DF⊥PB交PB于点F.则PB与平面EFD所成角为( )
ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a.点E为侧棱PC的中点,又作DF⊥PB交PB于点F.则PB与平面EFD所成角为( )
(A)30° (B)45° (C)60° (D)90°
D解析:建立如图所示的空间直角坐标系Dxyz,D为坐标原点.

则P(0,0,a),B(a,a,0),
 =(a,a,-a),
=(a,a,-a),
又 =(0,
=(0, ,
, ),
),
 ·
· =0+
=0+ -
- =0,
=0,
所以PB⊥DE,
由已知DF⊥PB,且DF∩DE=D,
所以PB⊥平面EFD,
所以PB与平面EFD所成角为90°.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ABC,如图2所示.
ABC,如图2所示.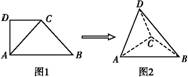
 ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足 时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)
ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足 时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可) 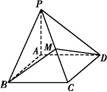

 =λ,MN∥平面ABC,求实数λ的值.
=λ,MN∥平面ABC,求实数λ的值. 的定义域时,大前提是当
的定义域时,大前提是当 有意义时,a≥0,小前提是
有意义时,a≥0,小前提是