题目内容
.如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D ABC,如图2所示.
ABC,如图2所示.
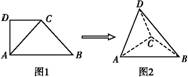
(1)求证:BC⊥平面ACD;
(2)求几何体D ABC的体积.
ABC的体积.
(1)证明:在题图1中,

可得AC=BC=2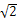 ,
,
从而AC2+BC2=AB2,
故AC⊥BC,
取AC的中点O,连接DO,
则DO⊥AC,
又平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,
DO⊂平面ADC,
从而DO⊥平面ABC,
∴DO⊥BC,
又AC⊥BC,AC∩DO=O,
∴BC⊥平面ACD.
(2)解:由(1)可知,BC为三棱锥B ACD的高,BC=2
ACD的高,BC=2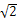 ,S△ACD=2,
,S△ACD=2,
∴ =
=
= S△ACD·BC
S△ACD·BC
= ×2×2
×2×2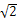
= .
.

练习册系列答案
相关题目
 是如图所示平面区域内的任意一点,则
是如图所示平面区域内的任意一点,则 的取值范围为 .
的取值范围为 .


 (D)6+3π+2
(D)6+3π+2
 A1B1C1D1中,O是BD1的中点,直线A1C交平面AB1D1于点M,则下列结论错误的是( )
A1B1C1D1中,O是BD1的中点,直线A1C交平面AB1D1于点M,则下列结论错误的是( )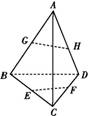
 ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
 ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a.点E为侧棱PC的中点,又作DF⊥PB交PB于点F.则PB与平面EFD所成角为( )
ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a.点E为侧棱PC的中点,又作DF⊥PB交PB于点F.则PB与平面EFD所成角为( )