题目内容
3.已知集合A={-1,0,1},B={y|y=|x|},则A∩B=( )| A. | {0} | B. | {1} | C. | {0,1} | D. | {-1,0,1} |
分析 分别示求出集合A,B,由此能求出A∩B.
解答 解:∵集合A={-1,0,1},B={y|y=|x|}={0,1},
∴A∩B={0,1}.
故选:C.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意并集性质的合理运用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
11.若函数f(x)=sinωx+$\sqrt{3}$cos(ωx+$\frac{π}{3}$)(ω>0)的最小正周期为π,则f(x)在[0,$\frac{π}{4}$]上的最大值为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
8.已知存在实数a,使得关于x的不等式$\sqrt{2x}-a≥\sqrt{9-5x}$恒成立,则a的最大值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
12.已知向量$\overrightarrow{AB}=({x,1}),({x>0}),\overrightarrow{AC}=({1,2}),|{\overrightarrow{BC}}|=\sqrt{5}$,则$\overrightarrow{AB},\overrightarrow{AC}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
13.已知$θ∈[{\frac{π}{2},π}]$,则$\sqrt{1+2sin({π+θ})sin({\frac{π}{2}-θ})}$=( )
| A. | sinθ-cosθ | B. | cosθ-sinθ | C. | ±(sinθ-cosθ) | D. | sinθ+cosθ |
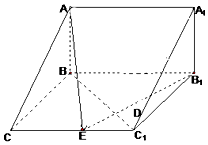 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,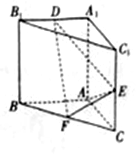 三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1
三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1