题目内容
6.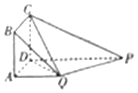 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD(Ⅰ)证明:PQ⊥QC
(Ⅱ)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
分析 (Ⅰ)推导出PQ⊥DC,PQ⊥QD,从而PQ⊥平面DCQ,由此能证明PQ⊥QC.
(Ⅱ)设AB=a,由题设知AQ为棱锥Q-ABCD的高,PQ为棱锥P-DCQ的高,由此能求出棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
解答 证明:(Ⅰ)∵四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD,
∴PDAQ为直角梯形,QA⊥平面ABCD,
平面PDAQ⊥平面ABCD,交线为AD,
又四边形ABCD为正方形,DC⊥AD,
∴DC⊥平面PDAQ,∴PQ⊥DC,
在直角梯形PDAQ中,DQ=PQ=$\frac{\sqrt{2}}{2}$PD,
∴PQ⊥QD,PQ⊥平面DCQ,
∴PQ⊥QC.
解:(Ⅱ)设AB=a,由题设知AQ为棱锥Q-ABCD的高,
∴棱锥Q-ABCD的体积V1=$\frac{1}{3}{a}^{3}$,
由(Ⅰ)知PQ为棱锥P-DCQ的高,
∵PQ=$\sqrt{2}a$,△DCQ的面积为$\frac{\sqrt{2}}{2}$a2,
∴棱锥P-DCQ的体积${V}_{2}=\frac{1}{3}{a}^{3}$,
∴棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值为1:1.
点评 本题考查线线垂直的证明,考查两个几何体的体积的比值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
1.已知球O的内接圆柱的体积是2π,底面半径为1,则球O的表面积为( )
| A. | 6π | B. | 8π | C. | 10π | D. | 12π |
11.若函数f(x)=sinωx+$\sqrt{3}$cos(ωx+$\frac{π}{3}$)(ω>0)的最小正周期为π,则f(x)在[0,$\frac{π}{4}$]上的最大值为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
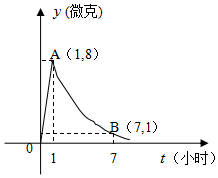 某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升中的含药量y(微克)与服药的时间t(小时)之间近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.
某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升中的含药量y(微克)与服药的时间t(小时)之间近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.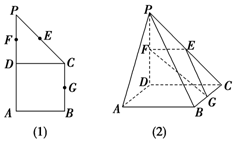 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).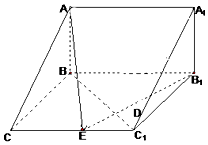 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,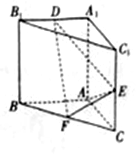 三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1
三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1