题目内容
4.点M(-3,4)是角α终边上一点,则有( )| A. | $sinα=-\frac{3}{5}$ | B. | $cosα=-\frac{4}{5}$ | C. | $tanα=-\frac{4}{3}$ | D. | 以上都不对 |
分析 求出OP,然后利用任意角的三角函数的定义直接求出sinα,cosα,tanα即可.
解答 解:点M(-3,4)是角α终边上一点,所以OM=$\sqrt{(-3)^{2}+{4}^{2}}$=5
由任意角的三角函数的定义可知sinα=$\frac{4}{5}$,cos$α=-\frac{3}{5}$,tan$α=-\frac{4}{3}$,
故选:C.
点评 本题考查任意角的三角函数的定义,考查计算能力,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知向量$\overrightarrow a=(2,-1)$,$\overrightarrow b=(3,1)$,则$2\overrightarrow a+3\overrightarrow b$=( )
| A. | (12,1) | B. | (13,5) | C. | (13,-1) | D. | (13,1) |
16.下列函数是奇函数的是( )
| A. | f(x)=x4 | B. | $f(x)=x+\frac{1}{x}$ | C. | f(x)=x3-1 | D. | $f(x)=\frac{1}{x^2}$ |
13.已知M(-2,0),N(1,3a),P(0,-1),Q(a,-2a),若MN⊥PQ,则a=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或1 |
14.若$\overrightarrow{a}$=(-3,4),$\overrightarrow{b}$=(2,-1),若($\overrightarrow{a}$-x$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$),则x等于( )
| A. | -23 | B. | -$\frac{7}{4}$ | C. | -$\frac{7}{3}$ | D. | $\frac{7}{2}$ |
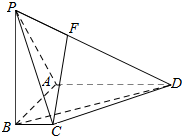 如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.
如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.