题目内容
9．已知x∈R，命题P：x≥0，命题$q：2x+\frac{1}{2x+1}≥1$，则p是q的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据基本不等式的性质以及充分必要条件的定义判断即可．
解答 解：若x≥0，则2x+1+$\frac{1}{2x+1}$≥2，即2x+$\frac{1}{2x+1}$≥1，是充分条件，
反之，不成立，
故选：A．
点评 本题考查了充分必要条件，考查基本不等式的性质，是一道基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
已知函数y=2sin（ωx+φ）（0＜ω＜2π）的部分图象如图所示，点A（$-\frac{π}{6}$，0），B、C是该图象与x轴的交点，过点B作直线交该图象于D、E两点，点F（$\frac{7π}{12}$，0）是f（x）的图象的最高点在x轴上的射影，则$（\overrightarrow{AD}-\overrightarrow{EA}）•（ω\overrightarrow{AC}）$的值是（ ）
4．如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别是（ ）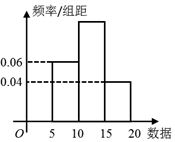
| A． | 12.5 11 | B． | 12.5 12 | C． | 12.5 13 | D． | 12.5 14 |
14．具有线性相关关系的变量x、y的一组数据如表所示．若y与
x的回归直线方程为$\stackrel{∧}{y}$=3x-$\frac{3}{2}$，则m的值是（ ）
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 6 |
| A． | 4 | B． | $\frac{9}{2}$ | C． | 5.5 | D． | 6 |
19．已知直线l1：ax+2y=0与直线l2：x+（a-1）y+a2-1=0平行，则实数a的值是（ ）
| A． | -1或2 | B． | 0或1 | C． | -1 | D． | 2 |