题目内容
17. 已知函数y=2sin(ωx+φ)(0<ω<2π)的部分图象如图所示,点A($-\frac{π}{6}$,0),B、C是该图象与x轴的交点,过点B作直线交该图象于D、E两点,点F($\frac{7π}{12}$,0)是f(x)的图象的最高点在x轴上的射影,则$(\overrightarrow{AD}-\overrightarrow{EA})•(ω\overrightarrow{AC})$的值是( )
已知函数y=2sin(ωx+φ)(0<ω<2π)的部分图象如图所示,点A($-\frac{π}{6}$,0),B、C是该图象与x轴的交点,过点B作直线交该图象于D、E两点,点F($\frac{7π}{12}$,0)是f(x)的图象的最高点在x轴上的射影,则$(\overrightarrow{AD}-\overrightarrow{EA})•(ω\overrightarrow{AC})$的值是( )| A. | 2π2 | B. | π2 | ||
| C. | 2 | D. | 以上答案均不正确 |
分析 根据函数y=2sin(ωx+φ)(ω>0)的部分图象,利用周期性求得ω,可得C、B的坐标,再根据线段EF关于点B对称,利用两个向量的加减法及其几何意义求得要求式子的值.
解答 解:根据函数y=2sin(ωx+φ)(ω>0)的部分图象可得
$\frac{3}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-(-$\frac{π}{6}$),
解得ω=2;
∵2•(-$\frac{π}{6}$)+φ=π,
∴φ=$\frac{4π}{3}$,
∴函数y=2sin(2x+$\frac{4π}{3}$),
可得C($\frac{5π}{6}$,0),
故AC的中点为B($\frac{π}{3}$,0);
由题意可得线段EF关于点B对称,则
($\overrightarrow{AD}$-$\overrightarrow{EA}$)•(ω$\overrightarrow{AC}$)=($\overrightarrow{AD}$+$\overrightarrow{AE}$)•(ω$\overrightarrow{AC}$)
=2$\overrightarrow{AB}$•2$\overrightarrow{AC}$
=4|AB|•|AC|
=4•$\frac{T}{2}$•T
=2T2
=2•${(\frac{2π}{2})}^{2}$
=2π2.
故选:A.
点评 本题主要考查了正弦函数的图象与性质,两个向量的加减法及其几何意义,是综合题.

练习册系列答案
相关题目
9.已知x∈R,命题P:x≥0,命题$q:2x+\frac{1}{2x+1}≥1$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
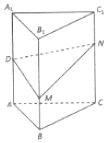 如图,正三棱柱ABC-A1B1C1的各棱长均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1上的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中正确的序号为②③④.
如图,正三棱柱ABC-A1B1C1的各棱长均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1上的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中正确的序号为②③④.