题目内容
19.已知函数f(x)=ax-lnx.(1)讨论函数f(x)的单调性;
(2)若f(x)>1,在区间(1,+∞)内恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)问题转化为a>$\frac{1+lnx}{x}$在区间(1,+∞)恒成立,设g(x)=$\frac{1+lnx}{x}$,根据函数的单调性求出a的范围即可.
解答 解:(1)f(x)的定义域是(0,+∞),
f′(x)=a-$\frac{1}{x}$=$\frac{ax-1}{x}$,
①a≤0时,f′(x)≤0,f(x)在(0,+∞)递减;
②a>0时,由f′(x)>0,解得:x>$\frac{1}{a}$,
由f′(x)<0,解得:0<x<$\frac{1}{a}$,
故f(x)在(0,$\frac{1}{a}$)递减,在($\frac{1}{a}$,+∞)递增;
(2)由f(x)>1,得ax-lnx-1>0,
即a>$\frac{1+lnx}{x}$在区间(1,+∞)恒成立,
设g(x)=$\frac{1+lnx}{x}$,则g′(x)=-$\frac{lnx}{{x}^{2}}$,
∵x>1,∴g′(x)<0,
故g(x)在(1,+∞)递减,
即$\frac{1+lnx}{x}$<1在区间(1,+∞)恒成立,
故a≥1.
点评 本题考查了函数的单调性问题,考查函数恒成立以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
4.命题p:直线l与抛物线C有且仅有一个公共点;命题q:直线l与抛物线C相切.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
11.已知椭圆$\frac{x^2}{5}+\frac{y^2}{m}=1$的离心率为$\frac{{\sqrt{10}}}{5}$,则m的值为( )
| A. | 3 | B. | $\frac{{5\sqrt{15}}}{3}$或$\sqrt{15}$ | C. | $\sqrt{5}$ | D. | $\frac{25}{3}$或3 |
9.已知x∈R,命题P:x≥0,命题$q:2x+\frac{1}{2x+1}≥1$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
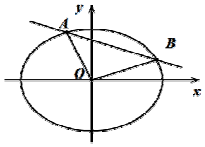 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点$P(1,\frac{3}{2})$,直线l:y=kx+m交椭圆E于不同的两点A,B,设线段AB的中点为M.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点$P(1,\frac{3}{2})$,直线l:y=kx+m交椭圆E于不同的两点A,B,设线段AB的中点为M.