题目内容
已知a，b，c为非零实数，且a2+b2+c2+1-m=0，
+
+
+1-2m=0．
（1）求证
+
+
≥
．
（2）求实数m的取值范围．
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
（1）求证
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
| 36 |
| a2+b2+c2 |
（2）求实数m的取值范围．
考点：不等式的证明
专题：选作题,不等式
分析：（1）由柯西不等式可得（
+
+
）（a2+b2+c2）≥（1+2+3）2，即可证明结论；
（2）利用（1）的结论，即可求实数m的取值范围．
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
（2）利用（1）的结论，即可求实数m的取值范围．
解答：
（1）证明：由柯西不等式可得（
+
+
）（a2+b2+c2）≥（1+2+3）2，
∴
+
+
≥
；
（2）解：∵a2+b2+c2+1-m=0，
+
+
+1-2m=0，
∴a2+b2+c2=m-1，
+
+
=2m-1，
∴（
+
+
）（a2+b2+c2）=（2m-1）（m-1）≥36，
∴2m2-3m-35≥0，
∴m≤-3.5或m≥5．
∵m≥1，
∴m≥5．
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
∴
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
| 36 |
| a2+b2+c2 |
（2）解：∵a2+b2+c2+1-m=0，
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
∴a2+b2+c2=m-1，
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
∴（
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
∴2m2-3m-35≥0，
∴m≤-3.5或m≥5．
∵m≥1，
∴m≥5．
点评：本题考查不等式的证明，考查柯西不等式，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
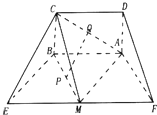如图，四边形ABEF是等腰梯形，AB∥EF，AF=BE=2，EF=4
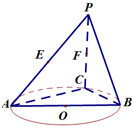如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．