题目内容
在△ABC中，a，b，c分别是内角A，B，C所对的边，c2=a2+b2-ab．
（1）求角C；
（2）若a=
，sinB=2sinA，求△ABC的面积．
（1）求角C；
（2）若a=
| 3 |
考点：余弦定理,正弦定理
专题：解三角形
分析：（1）在△ABC中，由条件利用余弦定理求得 cosC=
，结合0＜C＜π，可得C的值．
（2）由条件利用正弦定理得 b=2a=2
，再根据△ABC的面积为
ab•sinC计算求得结果．
| 1 |
| 2 |
（2）由条件利用正弦定理得 b=2a=2
| 3 |
| 1 |
| 2 |
解答：
解：（1）在△ABC中，∵c2=a2+b2-ab，
又由余弦定理得c2=a2+b2-2abcosC，∴cosC=
，∵0＜C＜π，∴C=
．
（2）∵sinB=2sinA，a=
∴由正弦定理得 b=2a=2
，
∴S△ABC=
absinC=
×
×2
×sin
=
．
又由余弦定理得c2=a2+b2-2abcosC，∴cosC=
| 1 |
| 2 |
| π |
| 3 |
（2）∵sinB=2sinA，a=
| 3 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
3
| ||
| 2 |
点评：本题主要考查正弦定理、余弦定理的应用，根据三角函数的值求角，属于中档题．
练习册系列答案
相关题目
调查某市出租车使用年限x和该年支出维修费用y（万元），得到数据如下：
则回归方程
=
x+
，必过定点（ ）
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
 |
| y |
|
| b |
|
| a |
| A、（2，3） |
| B、（3，4） |
| C、（4，5） |
| D、（5，6） |
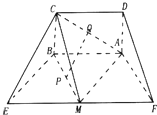如图，四边形ABEF是等腰梯形，AB∥EF，AF=BE=2，EF=4