题目内容
已知:集合A={x|2x≤256},集合B={x|log2x≥
}.
(1)求A∩B;
(2)若函数f(x)=log2(
)•log
(
)-m(x∈A∩B)的图象与x轴有交点,求实数m的取值范围.
| 1 |
| 2 |
(1)求A∩B;
(2)若函数f(x)=log2(
| x |
| 2 |
| 2 |
| ||
| 2 |
考点:函数的零点,交集及其运算
专题:函数的性质及应用
分析:(1)解不等式得出解集,(2)配方为f(x)=(log2x-
)2-
-m,
≤log2x≤3,根据函数单调性,求出最大值,最小值,列出不等式组即可.
| 3 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:
解:(1)∵A={x|2x≤256}={x|x≤8},
B={x|log2x≥
}={x|x≥
}.
∴A∩B={x|
≤x≤8}
(2)由(1)知:
≤x≤8∴
≤log2x≤3
f(x)=log2(
)•log
(
)-m
=(log2x-1)(log
-log
2)-m
=(log2x-1)(log2x-2)-m=(log2x-
)2-
-m
∴当log2x=
时,f(x)min=-
-m,
当log2x=3时,f(x)max=2-m
由题意可知:
∴-
≤m≤2
所以,实数m的取值范围是:[-
,2],
B={x|log2x≥
| 1 |
| 2 |
| 2 |
∴A∩B={x|
| 2 |
(2)由(1)知:
| 2 |
| 1 |
| 2 |
f(x)=log2(
| x |
| 2 |
| 2 |
| ||
| 2 |
=(log2x-1)(log
| 2 |
| x |
| 2 |
=(log2x-1)(log2x-2)-m=(log2x-
| 3 |
| 2 |
| 1 |
| 4 |
∴当log2x=
| 3 |
| 2 |
| 1 |
| 4 |
当log2x=3时,f(x)max=2-m
由题意可知:
|
∴-
| 1 |
| 4 |
所以,实数m的取值范围是:[-
| 1 |
| 4 |
点评:本题考查了函数的性质,不等式的解法,整体运用二次函数求解,属于中档题,难度较大.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
设函数f(x)=
+a是奇函数(a为常数),则f(x)<0的解集为( )
| 1 |
| 2x+1 |
| A、(0,+∞) | ||
| B、(1,+∞) | ||
| C、(-1,0)∪(0,1) | ||
D、(
|
设{an}是等差数列,{bn}是等比数列,Sn、Tn分别是数列{an}、{bn}的前n项和.若a3=b3,a4=b4,且
=7,则
的值为( )
| S5-S3 |
| T4-T2 |
| a5 |
| b3+b6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果b<a<0,那么下列不等式错误的是( )
| A、c+b<c+a | ||||
| B、a2<b2 | ||||
| C、bc2<ac2 | ||||
D、
|
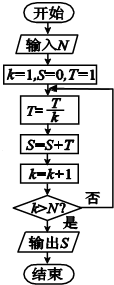 阅读如图的程序框图,解答以下问题:
阅读如图的程序框图,解答以下问题: