题目内容
10.已知f(x)=$\frac{a•2^x+a-2}{2^x+1}$是定义在[-2,2]上的奇函数.(1)求实数a的值,并求f(1)的值;
(2)证明:f(x)在定义域上为增函数;
(3)解不等式f(2x-1)<$\frac{1}{3}$.
分析 (1)根据函数奇偶性的性质建立方程关系即可得到结论.
(2)利用函数单调性的定义进行证明即可.
(3)利用函数奇偶性和单调性的关系将不等式进行转化求解.
解答 解:(1)方法一:∵f(x)是奇函数,
∴f(-x)=-f(x),
又f(x)=$\frac{a•({2}^{x}+1)-2}{{2}^{x}+1}$=a-$\frac{2}{{2}^{x}+1}$,
∴a-$\frac{2}{{2}^{-x}+′1}$=-a+$\frac{2}{{2}^{x}+1}$,
∴2a=$\frac{2}{\frac{1}{{2}^{x}}+1}$+$\frac{2}{{2}^{x}+1}$=$\frac{2•{2}^{x}}{{2}^{x}+1}$+$\frac{2}{{2}^{x}+1}$=2,∴a=1.
方法二:∵f(x)是[-2,2]上的奇函数,∴f(0)=a-1=0,∴a=1.
即f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,∴f(1)=$\frac{1}{3}$.
(2)证明如下:由(1)知f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$( x∈[-2,2]).任取-∞<x1<x2<+∞,
∵f(x1)-f(x2)=$\frac{{2}^{{x}_{1}}-1}{{2}^{{x}_{1}}+1}$-$\frac{{2}^{{x}_{2}}-1}{{2}^{{x}_{2}}+1}$=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$.
∵-2≤x1<x2≤2,∴2x1<2x2.
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴f(x)在定义域上为增函数.
(3)∵f(1)=$\frac{1}{3}$.
∴不等式f(2x-1)<$\frac{1}{3}$.等价为f(2x-1)<f(1),
∵f(x)定义在[-2,2]上的奇函数且单调递增.
∴-2≤2x-1<1,
即$-\frac{1}{2}$≤x<1,
即不等式的解集为[$-\frac{1}{2}$,1).
点评 本题主要考查函数奇偶性和单调性的判断和应用,利用函数奇偶性和单调性的定义和性质是解决本题的关键.

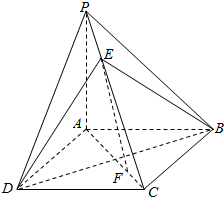 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,点E、F在PC、AC上,PE=$\frac{1}{4}$PC.
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,点E、F在PC、AC上,PE=$\frac{1}{4}$PC.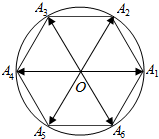 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.