题目内容
(本小题满分12分)如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.

(1)求证:BC⊥平面VAC;
(2)若直线AM与平面VAC所成角为 .求三棱锥B-ACM的体积.
.求三棱锥B-ACM的体积.
(1))祥见解析;(2)
【解析】
试题分析:(1)由线面垂直得VC⊥BC,由直径性质得AC⊥BC,由此能证明BC⊥平面VAC.(2)首先由(1)作出直线AM与平面VAC所成的角:取VC的中点N,连接MN,AN,则MN∥BC,由(I)得BC⊥平面VAC,所以MN⊥平面VAC,则∠MAN为直线AM与平面VAC所成的角.即∠MAN= ,所以MN=AN;这样就可求出AC的长,且
,所以MN=AN;这样就可求出AC的长,且 而求得体积.
而求得体积.
试题解析:(1)证明:因为VC⊥平面ABC, ,所以VC⊥BC,又因为点C为圆O上一点,且AB为直径,所以AC⊥BC,又因为VC,AC
,所以VC⊥BC,又因为点C为圆O上一点,且AB为直径,所以AC⊥BC,又因为VC,AC 平面VAC,VC∩AC=C,所以BC⊥平面VAC. 4分
平面VAC,VC∩AC=C,所以BC⊥平面VAC. 4分
(2)如图,取VC的中点N,连接MN,AN,则MN∥BC,由(I)得BC⊥平面VAC,所以MN⊥平面VAC,则∠MAN为直线AM与平面VAC所成的角.即∠MAN= ,所以MN=AN; 6分
,所以MN=AN; 6分

令AC=a,则BC= ,MN=
,MN= ;因为VC=2,M为VC中点,所以AN=
;因为VC=2,M为VC中点,所以AN= , 所以,
, 所以, =
= ,解得a=1 10分
,解得a=1 10分
因为MN∥BC,所以
 12分
12分
考点:1. 直线与平面垂直的判定;2. 棱柱、棱锥、棱台的体积;3. 直线与平面所成的角.

练习册系列答案
相关题目
 是
是 所在平面上的两个定点,且满足
所在平面上的两个定点,且满足
 ,若
,若 ,则正实数
,则正实数 = .
= . ,若
,若 .
. 的焦点到其渐近线的距离等于2,抛物线
的焦点到其渐近线的距离等于2,抛物线 的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为
的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为 B.
B.
 D.
D.
 则
则 的值为
的值为 ,
, ,则
,则 的最小值为 ;
的最小值为 ;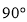 B.
B.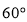
 C.
C. D.
D.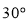
 是定义域为
是定义域为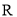 的偶函数. 当
的偶函数. 当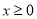 时,
时, 若关于
若关于 的方程
的方程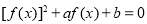 (
(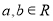 ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数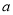 的取值范围是( )
的取值范围是( )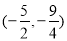 B.
B.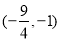 C.
C.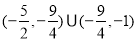 D.
D.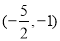
 的力能使弹簧伸长
的力能使弹簧伸长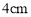 ,则把弹簧从平衡位置拉长
,则把弹簧从平衡位置拉长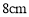 (在弹性限度内)时所做的功为 (单位:焦耳).
(在弹性限度内)时所做的功为 (单位:焦耳).