题目内容
在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成角为60°,E为PC的中点,则异面直线PA与BE所成角为 ( )
A.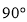 B.
B.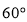
 C.
C. D.
D.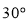
C
【解析】
试题分析:连接AC,BD交于点O,连接OE,OP;因为E为PC中点,所以OE∥PA,

所以∠OEB即为异面直线PA与BE所成的角.
因为四棱锥P-ABCD为正四棱锥,
所以PO⊥平面ABCD,
所以AO为PA在面ABCD内的射影,所以∠PAO即为PA与面ABCD所成的角,即∠PAO=60°,
因为PA=2,所以OA=OB=1,OE=1.
所以在直角三角形EOB中∠OEB=45°,即面直线PA与BE所成的角为45°.
故选:C.
考点:异面直线及其所成的角.

练习册系列答案
相关题目
 的定义域是 .
的定义域是 . 且斜率为k的直线
且斜率为k的直线 与圆
与圆 相交于P、Q两点,则
相交于P、Q两点,则 的值为
的值为
 .求三棱锥B-ACM的体积.
.求三棱锥B-ACM的体积. 是定义域为
是定义域为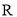 的偶函数. 当
的偶函数. 当 时,
时, 若关于
若关于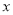 的方程
的方程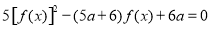 (
( ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数 的取值范围是( )
的取值范围是( ) B.
B.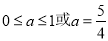
 D.
D. 或
或
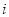 是虚数单位,则复数
是虚数单位,则复数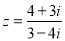 的虚部是( )
的虚部是( )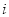 C.
C.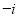 D.1
D.1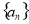 中,
中,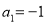 ,公差
,公差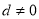 且
且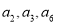 成等比数列,前
成等比数列,前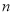 项的和为
项的和为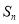 .
.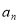 及
及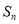 ;
;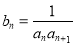 ,
,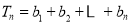 ,求
,求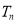 .
. ,点
,点 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
 的方程;
的方程; 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹 相交于
相交于 两点,直线
两点,直线 的斜率分别为
的斜率分别为
 .△
.△ 的面积为
的面积为 ,以
,以 为直径的圆的面积分别为
为直径的圆的面积分别为 .若
.若 恰好构成等比数列,求
恰好构成等比数列,求 的取值范围.
的取值范围. ,使得
,使得


 是
是 的充分不必要条件
的充分不必要条件