题目内容
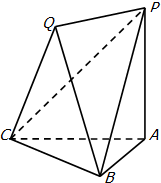 (文)在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.
(文)在空间几何体PQ-ABC中,PA⊥平面ABC,平面QBC⊥平面ABC,AB=AC,QB=QC.(1)求证:PA∥平面QBC;
(2)如果PQ⊥平面QBC,求证:VQ-PBC=VP-ABC.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)取BC中点D,连QD,证明QD⊥平面ABC,利用PA⊥平面ABC,即可证明PA∥平面QBC;
(2)证明AD⊥平面QBC,利用PQ⊥平面QBC,可得PQ∥AD,四边形APQD是矩形,即可证明VQ-PBC=VP-ABC.
(2)证明AD⊥平面QBC,利用PQ⊥平面QBC,可得PQ∥AD,四边形APQD是矩形,即可证明VQ-PBC=VP-ABC.
解答:
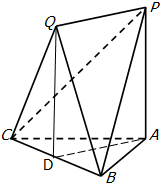 证明:(1)如图,取BC中点D,连QD,
证明:(1)如图,取BC中点D,连QD,
由QB=QC得QD⊥BC,∵平面QBC⊥平面ABC,
∴QD⊥平面ABC,
又∵PA⊥平面ABC,
∴QD∥PA,
又∵QD?平面QBC,
∴PA∥平面QBC.
(2)连接AD,则AD⊥BC.
∵平面QBC⊥平面ABC,面QBC∩面ABC=BC,
∴AD⊥平面QBC.
又∵PQ⊥平面QBC,∴PQ∥AD.
又由(1)知,四边形APQD是矩形,
∴PQ=AD,PA=QD.
∴VQ-PBC=VP-QBC=
•(
BC•QD)•PQ,
而VP-ABC=
•(
BC•AD)•PA,则VQ-PBC=VP-ABC.
 证明:(1)如图,取BC中点D,连QD,
证明:(1)如图,取BC中点D,连QD,由QB=QC得QD⊥BC,∵平面QBC⊥平面ABC,
∴QD⊥平面ABC,
又∵PA⊥平面ABC,
∴QD∥PA,
又∵QD?平面QBC,
∴PA∥平面QBC.
(2)连接AD,则AD⊥BC.
∵平面QBC⊥平面ABC,面QBC∩面ABC=BC,
∴AD⊥平面QBC.
又∵PQ⊥平面QBC,∴PQ∥AD.
又由(1)知,四边形APQD是矩形,
∴PQ=AD,PA=QD.
∴VQ-PBC=VP-QBC=
| 1 |
| 3 |
| 1 |
| 2 |
而VP-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题考查线面平行,考查体积的计算,考查学生分析解决问题的能力,正确运用线面平行的判定定理是关键.

练习册系列答案
相关题目
已知变量x与y之间一组对应数据如表格所示,经计算它们的回归直线方程为
=2.3x+0.8,定义ei=yi-
i为第i组数据的残差,如果要去除残差绝对值最大的那组数据,则应该去除( )
 |
| y |
 |
| y |
| 序号i | 1 | 2 | 3 | 4 |
| xi | 0 | 1 | 2 | 3 |
| yi | 1 | 3 | 5 | 8 |
| A、第1组 | B、第2组 |
| C、第3组 | D、第4组 |
直线l过点P(1,3),且与x、y轴正半轴围成的三角形的面积等于6的直线方程是( )
| A、3x+y-6=0 |
| B、x+3y-10=0 |
| C、3x-y=0 |
| D、x-3y+8=0 |
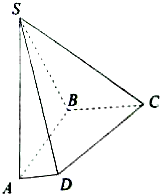 如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,SA⊥平面ABCD,且AD∥BC,AB⊥AD,BC=2AD=2,AB=AS=
如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,SA⊥平面ABCD,且AD∥BC,AB⊥AD,BC=2AD=2,AB=AS=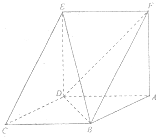 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD. 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC.