题目内容
三棱锥P-ABC的四个顶点均在半径为2的球面上,且AB=BC=CA=2
,平面PAB⊥平面ABC,则三棱锥P-ABC的体积的最大值为( )
| 3 |
| A、4 | ||
| B、3 | ||
C、4
| ||
D、3
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:运用题意判断出三棱锥P-ABC的体积的最大值时,几何体的性质,在求解体积的值.
解答:
解:根据题意:半径为2的球面上,且AB=BC=CA=2
,
△ABC为截面为大圆上三角形,
设圆形为O,AB的中点为N,ON═
=1
∵平面PAB⊥平面ABC,
∴三棱锥P-ABC的体积的最大值时,PN⊥AB,PN⊥平面ABC,
PB=
=
,
∴三棱锥P-ABC的体积的最大值为
×
×(2
)2×
=3,
故选:B
| 3 |
△ABC为截面为大圆上三角形,
设圆形为O,AB的中点为N,ON═
| 22-3 |
∵平面PAB⊥平面ABC,
∴三棱锥P-ABC的体积的最大值时,PN⊥AB,PN⊥平面ABC,
PB=
| 22-1 |
| 3 |
∴三棱锥P-ABC的体积的最大值为
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 3 |
故选:B
点评:本题考查了几何体的体积计算,探索几何体的位置情况,属于中档题.

练习册系列答案
相关题目
设F是双曲线
-
=1(a>0,b>0)的左焦点,A(a,b),P是双曲线右支上的动点.若|PF|+|PA|的最小值为3a,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1+
| ||||
C、
| ||||
D、
|
已知点A(1,2),B(3,2),以线段AB为直径作圆C,则直线l:x+y-3=0与圆C的位置关系是( )
| A、相交且过圆心 | B、相交但不过圆心 |
| C、相切 | D、相离 |
如果函数f(x)=x2-(a-1)x+3在区间(4,+∞)上是增函数,那么实数a的取值范围是( )
| A、(-∞,9] |
| B、[5,+∞) |
| C、[9,+∞) |
| D、(-∞,5] |
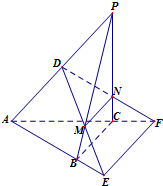 如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.
如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.