题目内容
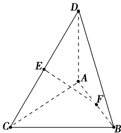 已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.
已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.(1)证明AC⊥EF;
(2)求二面角C-DB-A的正切值.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)取AC中点G,连接EG,GF,由已知条件推导出EG∥DA,GF∥CB,由此得到AC⊥平面EGF,从而能证明AC⊥EF.
(2)连接CF,在平面DAB中作FH⊥DB于点H,连接CH.由已知条件推导出∠FHC就是二面角CDBA的平面角,由此能求出二面角C-DB-A的正切值.
(2)连接CF,在平面DAB中作FH⊥DB于点H,连接CH.由已知条件推导出∠FHC就是二面角CDBA的平面角,由此能求出二面角C-DB-A的正切值.
解答:
(1)证明:取AC中点G,连接EG,GF,
因为E是DC的中点,F是AB的中点,
所以EG∥DA,GF∥CB,
因为DA⊥平面ABC,AC?平面ABC,所以DA⊥AC,
因此AC⊥EG,因为AC⊥CB,所以AC⊥GF,
EG?平面EGF,GF?平面EGF,EG∩GF=G,
所以AC⊥平面EGF,EF?平面EGF,所以AC⊥EF.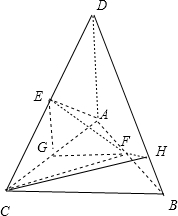
(2)解:连接CF,在平面DAB中作FH⊥DB于点H,
连接CH.因为AC=CB,F是AB的中点,所以CF⊥AB,
因为DA⊥平面ABC,CF?平面ABC,所以CF⊥DA,
DA∩AB=A,DA?平面DAB,AB?平面DAB,所以CF⊥平面DAB,
DB?平面DAB,所以DB⊥CF,因此DB⊥平面FCH,DB⊥CH,
所以∠FHC就是二面角CDBA的平面角.
因为
=
,所以FH=
•DA=
×2=
×2=
,
在直角三角形CFH中,CF=
,∠CFH=
,
所以tan∠CHF=
=
=
.
所以二面角C-DB-A的正切值为
.
因为E是DC的中点,F是AB的中点,
所以EG∥DA,GF∥CB,
因为DA⊥平面ABC,AC?平面ABC,所以DA⊥AC,
因此AC⊥EG,因为AC⊥CB,所以AC⊥GF,
EG?平面EGF,GF?平面EGF,EG∩GF=G,
所以AC⊥平面EGF,EF?平面EGF,所以AC⊥EF.

(2)解:连接CF,在平面DAB中作FH⊥DB于点H,
连接CH.因为AC=CB,F是AB的中点,所以CF⊥AB,
因为DA⊥平面ABC,CF?平面ABC,所以CF⊥DA,
DA∩AB=A,DA?平面DAB,AB?平面DAB,所以CF⊥平面DAB,
DB?平面DAB,所以DB⊥CF,因此DB⊥平面FCH,DB⊥CH,
所以∠FHC就是二面角CDBA的平面角.
因为
| FH |
| DA |
| FB |
| DB |
| FB |
| DB |
| ||
|
| ||||
|
| ||
| 3 |
在直角三角形CFH中,CF=
| 2 |
| π |
| 2 |
所以tan∠CHF=
| CF |
| FH |
| ||||
|
| 3 |
所以二面角C-DB-A的正切值为
| 3 |
点评:本题考查异面直线垂直的证明,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
已知a,b是实数,则“a+b>1”是“2a>(
)b”的( )
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
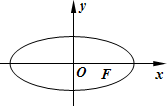 已知椭圆
已知椭圆