题目内容
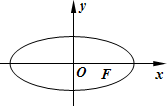 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| OP |
| OA |
| OB |
(1)求椭圆标准方程;
(2)当λ=1,且直线AB过F点且垂直于x轴时,求过A,B,P三点的外接圆方程;
(3)若直线OA与OB的斜率乘积kOA•kOB=-
| 1 |
| 2 |
| 2 |
| 2 |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:(1)将已知条件代入离心率e=
,a2=b2+c2得a,b的值,方程可求;
(2)由直线AB过F点且垂直于x轴,可得AB的方程,将x=1代入椭圆方程易得A,B的坐标,继而求出P点坐标,然后利用待定系数法求出圆的一般式方程;
(3)总体思路是:先假设λ存在,然后想办法构造一个关于λ的方程.即先将条件“直线OA与OB的斜率乘积kOA•kOB=-
,动点P满足
=
+λ
,”结合一下,可以找到一个关于x1,x2,y1,y2,λ的关系式,化简后,再结合“P满足PG+PQ=4,其中G(-
,0),Q(
,0)”可看出,P的轨迹应该是一个椭圆,再利用椭圆的定义最终得到关于λ的方程,解之即可.
| c |
| a |
(2)由直线AB过F点且垂直于x轴,可得AB的方程,将x=1代入椭圆方程易得A,B的坐标,继而求出P点坐标,然后利用待定系数法求出圆的一般式方程;
(3)总体思路是:先假设λ存在,然后想办法构造一个关于λ的方程.即先将条件“直线OA与OB的斜率乘积kOA•kOB=-
| 1 |
| 2 |
| OP |
| OA |
| OB |
| 2 |
| 2 |
解答:
解:( I)有题设可知:
∴a=
又b2=a2-c2,∴b2=1,
∴椭圆标准方程为
+y2=1
(2)由题意可知直线AB方程为x=1,代入
+y2=1解得A(1,
),B(1,-
),P(2,0),
设圆的方程x2+y2+Dx+Ey+F=0,将A,B,P三点代入得
,
解得D=-
,E=0,F=1,
所以圆的方程是x2+y2-
x+1=0
(3)设P(x,y),A(x1,y1),B(x2,y2),
则由
=
+λ
得
(x,y)=(x1,y1)+λ(x2,y2)=(x1+λx2,y1+λy2),
即x=x1+λx2,y=y1+λy2.
∵点A、B在椭圆x2+2y2=2上,
∴x
+2y
=2,x
+2y
+=2,故x2+2y2=(x
+λ2x
+2λx1x2)+2(y
+λ2y
+2λy1y2)=(x
+2y
)+λ2(x
+2yx)+2λ(x1x2+2y1y2)
=2+2λ2+2λ(x1x2+2y1y2).
设kOA,kOB分别为直线OA,OB的斜率,
由题设条件知kOA•kOB=
=-
,
∴x1x2+2y1y2=0,∴x2+2y2=2+2λ2.即
+
=1
∴P点是椭圆
+
=1上的点,
设该椭圆的左、右焦点为G,Q,则由椭圆的定义PG+PQ=4为定值.
所以4=2
,∴λ=±1,
此时两焦点的坐标为 G(-
,0),Q(
,0)
∴存在λ=±1使得PG+PQ=4
|
∴a=
| 2 |
∴椭圆标准方程为
| x2 |
| 2 |
(2)由题意可知直线AB方程为x=1,代入
| x2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
设圆的方程x2+y2+Dx+Ey+F=0,将A,B,P三点代入得
|
解得D=-
| 5 |
| 2 |
所以圆的方程是x2+y2-
| 5 |
| 2 |
(3)设P(x,y),A(x1,y1),B(x2,y2),
则由
| OP |
| OA |
| OB |
(x,y)=(x1,y1)+λ(x2,y2)=(x1+λx2,y1+λy2),
即x=x1+λx2,y=y1+λy2.
∵点A、B在椭圆x2+2y2=2上,
∴x
2 1 |
2 1 |
2 2 |
2 2 |
2 1 |
2 2 |
2 1 |
2 2 |
2 1 |
2 1 |
2 2 |
=2+2λ2+2λ(x1x2+2y1y2).
设kOA,kOB分别为直线OA,OB的斜率,
由题设条件知kOA•kOB=
| y1y2 |
| x1x2 |
| 1 |
| 2 |
∴x1x2+2y1y2=0,∴x2+2y2=2+2λ2.即
| x2 |
| 2+2λ2 |
| y2 |
| 1+λ2 |
∴P点是椭圆
| x2 |
| 2+2λ2 |
| y2 |
| 1+λ2 |
设该椭圆的左、右焦点为G,Q,则由椭圆的定义PG+PQ=4为定值.
所以4=2
| 2+2λ2 |
此时两焦点的坐标为 G(-
| 2 |
| 2 |
∴存在λ=±1使得PG+PQ=4
点评:椭圆的方程一般采用定义结合离心率公式、和a,b,c的关系式来求;圆的方程主要是待定系数法,知道点的坐标或者与半径,圆心有关的条件,将之代入圆的方程得到关于系数的方程组;第三问有一定难度,但一般思路仍然是将已知条件坐标化,然后消元、化简,要充分理解所给条件的意义,比如本题中的条件“动点P满足PG+PQ=4,其中G(-
,0),Q(
,0)”就是椭圆的定义,这是最终解决本题的关键.
| 2 |
| 2 |

练习册系列答案
相关题目
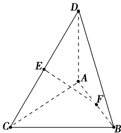 已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.
已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.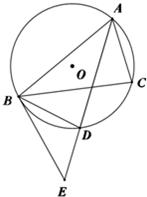 如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.
如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.