题目内容
已知函数f(x)=
ax3-
(a+1)x2+bx(a,b∈R,a≠1,a>0)在x=1时取得极值.
(1)求b的值;
(2)求f(x)的单调减区间.
| 1 |
| 3 |
| 1 |
| 2 |
(1)求b的值;
(2)求f(x)的单调减区间.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)依题意,得f′(x)=ax2-(a+1)x+b由于x=1为函数的一个极值点,则f′(1)=0,得b=1.
(2)由(1)得;f′(x)=ax2-(a+1)x+1,①当0<a<1时,1<
,②当a>1时,
<1,令f′(x)<0,解不等式求出即可.
(2)由(1)得;f′(x)=ax2-(a+1)x+1,①当0<a<1时,1<
| 1 |
| a |
| 1 |
| a |
解答:
解:(1)依题意,得f′(x)=ax2-(a+1)x+b
由于x=1为函数的一个极值点,
则f′(1)=0,
解得b=1.
(2)由(1)得;f′(x)=ax2-(a+1)x+1,
①当0<a<1时,1<
,
令f′(x)<0,
∴不等式的解集为1<x<
;
②当a>1时,
<1,
令f′(x)<0,
∴不等式的解集为
<x<1;
综上,当0<a<1时,f(x)的单调减区间为(1,
);
当a>1时,f(x)的单调减区间为(
,1).
由于x=1为函数的一个极值点,
则f′(1)=0,
解得b=1.
(2)由(1)得;f′(x)=ax2-(a+1)x+1,
①当0<a<1时,1<
| 1 |
| a |
令f′(x)<0,
∴不等式的解集为1<x<
| 1 |
| a |
②当a>1时,
| 1 |
| a |
令f′(x)<0,
∴不等式的解集为
| 1 |
| a |
综上,当0<a<1时,f(x)的单调减区间为(1,
| 1 |
| a |
当a>1时,f(x)的单调减区间为(
| 1 |
| a |
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
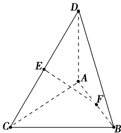 已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.
已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.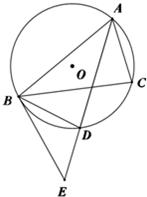 如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.
如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.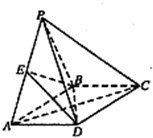 如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAB是正三角形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAB是正三角形,AB=2,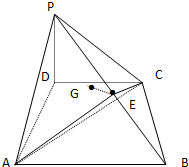 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠CDA=∠DAB=90°,PD⊥底面ABCD,PD=AD,CD=1,AB=2,E是PB中点,点E在平面ACP上的射影是△ACP
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠CDA=∠DAB=90°,PD⊥底面ABCD,PD=AD,CD=1,AB=2,E是PB中点,点E在平面ACP上的射影是△ACP