题目内容
已知数列{an}满足奇数项a1,a3,a5,…成等差数列{a2n-1}(n∈N+),而偶数项a2,a4,a6,…成等比数列{a2n}(n∈N+),且a1=1,a2=2,a2,a3,a4,a5成等差数列,数列{an}的前n项和为Sn.
(Ⅰ)求Sn;
(Ⅱ)设bn=
,试比较bn+1与bn的大小.
(Ⅰ)求Sn;
(Ⅱ)设bn=
| S2n |
| 2n |
考点:数列的求和,等差数列与等比数列的综合
专题:
分析:(Ⅰ)先利用等差数列及等比数列的定义求得a2n-1=2n-1,a2n=2n,进而利用等差数列及等比数列的求和公式分别求得奇数项的和及偶数项的和,即得结论.注意分类讨论.
(Ⅱ)利用(Ⅰ)的结论得bn+1-bn=
-
=
.即得结论.
(Ⅱ)利用(Ⅰ)的结论得bn+1-bn=
| (n+1)2+2n+2-2 |
| 2n+1 |
| n2+2n+1-2 |
| 2n |
| 4-(n-1)2 |
| 2n+1 |
解答:
解:(Ⅰ)设等差数列{a2n-1}(n∈N+)的公差为d,等比数列{a2n}(n∈N+)的公比为q,
则2(1+d)=2+2q,4q=(1+d)+(1+2d),解得q=d=2.…(2分)
于是a2n-1=2n-1,a2n=2n,即数列的通项an=
…(4分)
于是当n为偶数时,数列奇数项的和为[
]×
=
,偶数项的和为
=2
+1-2,
故Sn=
+2
+1-2.…(6分)
当n为奇数时,Sn=Sn-1+an=
+2
-2+n=2
+
.
于是Sn=
…(8分)
(Ⅱ)由(Ⅰ)得bn=
=
,bn+1-bn=
-
=
.…(10分)
当n≤3时,bn+1≥bn;当n>3时,bn+1<bn.…(13分)
则2(1+d)=2+2q,4q=(1+d)+(1+2d),解得q=d=2.…(2分)
于是a2n-1=2n-1,a2n=2n,即数列的通项an=
|
于是当n为偶数时,数列奇数项的和为[
1+(2×
| ||
| 2 |
| n |
| 2 |
| n2 |
| 4 |
2(1-2
| ||
| 1-2 |
| n |
| 2 |
故Sn=
| n2 |
| 4 |
| n |
| 2 |
当n为奇数时,Sn=Sn-1+an=
| (n-1)2 |
| 4 |
| n+1 |
| 2 |
| n+1 |
| 2 |
| n2+2n-7 |
| 4 |
于是Sn=
|
(Ⅱ)由(Ⅰ)得bn=
| S2n |
| 2n |
| n2+2n+1-2 |
| 2n |
| (n+1)2+2n+2-2 |
| 2n+1 |
| n2+2n+1-2 |
| 2n |
| 4-(n-1)2 |
| 2n+1 |
当n≤3时,bn+1≥bn;当n>3时,bn+1<bn.…(13分)
点评:本题主要考查等差数列及等比数列的定义性质和求和公式的应用,考查学生的分类讨论思想及运算求解能力,属中档题.

练习册系列答案
相关题目
已知复数z=(a2-1)+(a-2)i(a∈R)是纯虚数,则a=( )
| A、1 | B、-1 | C、-1或1 | D、2 |
一个几何体按比例绘制的三视图如图所示(单位:m)
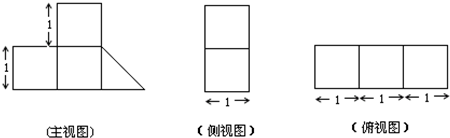
则该几何体的表面积为( )m3.

则该几何体的表面积为( )m3.
| A、14 | ||
| B、15 | ||
C、14+
| ||
D、15+
|
已知a∈R,则“a=-1”是“a2-1+(a-1)i为纯虚数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,某广场中间有一块扇形绿地OAB,其中O为扇形OAB所在圆的圆心,∠AOB=60°,扇形绿地OAB的半径为r.广场管理部门欲在绿地上修建观光小路:在
如图,某广场中间有一块扇形绿地OAB,其中O为扇形OAB所在圆的圆心,∠AOB=60°,扇形绿地OAB的半径为r.广场管理部门欲在绿地上修建观光小路:在