题目内容
如图，某广场中间有一块扇形绿地OAB，其中O为扇形OAB所在圆的圆心，∠AOB=60°，扇形绿地OAB的半径为r．广场管理部门欲在绿地上修建观光小路：在 |
| AB |
（1）设∠COD=θ，试将CD与CE的总长s表示成θ的函数s=f（θ）；
（2）当θ取何值时，s取得最大值？求出s的最大值．
考点：三角函数中的恒等变换应用,弧度制
专题：三角函数的图像与性质
分析：（1）设扇形的半径为r．在△ODC 中，∠AOB=60°，∠CDO=120°，利用正弦定理得
=
，可求得CD与CE，从而可得函数s=f（θ）；
（2）利用三角恒等变换，可求得s=
rsinθ+
rsin（
-θ）=
rsin（
+θ），θ∈（0，
）；利用正弦函数的单调性与最值即可求得s的最大值．
| r |
| sin∠CDO |
| CD |
| sin∠COD |
（2）利用三角恒等变换，可求得s=
2
| ||
| 3 |
2
| ||
| 3 |
| π |
| 3 |
2
| ||
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：
解：（1）设扇形的半径为r，
在△ODC 中，∠AOB=60°，则∠CDO=120°，由正弦定理得
=
，
∴CD=
rsinθ，同理CE=
rsin（
-θ），
∴s=f（θ）=
rsinθ+
rsin（
-θ），θ∈（0，
）；
（2）∵s=
rsinθ+
rsin（
-θ）
=
rsinθ+
×
rcosθ-
×
rsinθ
=
rsinθ+rcosθ=
rsin（
+θ），θ∈（0，
）；
∵θ∈（0，
），
∴
+θ∈（
，
），
∴当
+θ=
，即θ=
时，smax=f（
）=
r．
在△ODC 中，∠AOB=60°，则∠CDO=120°，由正弦定理得
| r |
| sin∠CDO |
| CD |
| sin∠COD |
∴CD=
2
| ||
| 3 |
2
| ||
| 3 |
| π |
| 3 |
∴s=f（θ）=
2
| ||
| 3 |
2
| ||
| 3 |
| π |
| 3 |
| π |
| 3 |
（2）∵s=
2
| ||
| 3 |
2
| ||
| 3 |
| π |
| 3 |
=
2
| ||
| 3 |
| ||
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
=
| ||
| 3 |
2
| ||
| 3 |
| π |
| 3 |
| π |
| 3 |
∵θ∈（0，
| π |
| 3 |
∴
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
2
| ||
| 3 |
点评：本题考查三角函数中的恒等变换应用，考查正弦定理与两角差与两角和的正弦，考查运算求解能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
定义区间[a，b]的长度为b-a．若[
，
]是函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜π）一个长度最大的单调递减区间，则（ ）
| π |
| 4 |
| π |
| 2 |
A、ω=8，φ=
| ||
B、ω=8，φ=-
| ||
C、ω=4，φ=
| ||
D、ω=4，φ=-
|
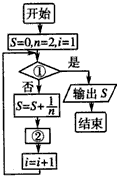如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 108 |
| A、i＞108，n=n+1 |
| B、i＞108，n=n+2 |
| C、i＞54，n=n+2 |
| D、i≤54，n=n+2 |
已知（ax+1）5的展开式中x3的系数是10，则实数a的值是（ ）
| A、1 | ||
B、
| ||
| C、-1 | ||
| D、2 |
如图，P是圆O外一点，过P引圆O的两条割线PAB、PCD，PA=AB=