题目内容
15.现有清华、北大、上海交大三所大学的招生负责人各一人来我市宣讲2017年高考自主招生政策,我市四所重点中学必须且只能邀请其中一所大学的负责人,且邀请其中任何一所大学的负责人是等可能的.(Ⅰ)求恰有两所重点中学邀请了清华招生负责人的概率;
(Ⅱ)设被邀请的大学招生负责人的个数为ξ,求ξ分布列与期望.
分析 (Ⅰ)设每所重点中学邀请负责人为一次实验这是4次独立重复实验,利用独立重复实验概率计算法则即可‘
(Ⅱ) ξ的所有可能值为1,2,3,求出相应的概率,写出分布列,求出期望.
解答 解:(Ⅰ)设每所重点中学邀请负责人为一次实验这是4次独立重复实验,记“邀请清华负责人”为事件A则$p(A)=\frac{1}{3}$从而设
恰有“两所重点中学邀请清华负责人”为事件B
则$P(B)=C_4^2{(\frac{1}{3})^2}•{(\frac{2}{3})^2}=\frac{8}{27}$…(4分)
(另解:$P=\frac{C_4^2×2×2}{3^4}=\frac{8}{27}$)
(Ⅱ)
| ξ | 1 | 2 | 3 |
| P | $\frac{1}{27}$ | $\frac{14}{27}$ | $\frac{4}{9}$ |
点评 本题考查了独立重复实验随机变量的概率、期望的计算,属于基础题.

练习册系列答案
相关题目
20.已知关于x的一次函数y=mx+n,设m∈{-1,1,2},n∈{-2,2},则函数y=mx+n是增函数的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
4.8名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得2分,平局各得1分,负者得0分,并按总得分由高到低进行排序.比赛结束后,8名选手的得分各不相同,且第二名的得分与最后四名选手得分之和相等.则第二名选手的得分是( )
| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
5.在△ABC中,a=1,b=$\sqrt{3}$,A=30°,则角C=( )
| A. | 60° | B. | 30°或90° | C. | 30° | D. | 60°或120° |
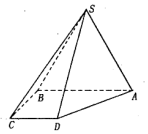 如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.
如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.