题目内容
7.已知函数$f(x)=2sin(\frac{π}{2}-x)•sinx+\sqrt{3}$cos2x.(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在$[-\frac{π}{12},\;\frac{π}{6}]$上的最大值.
分析 (1)根据三角函数的辅助角公式进行化简结合三角函数的性质进行求解即可.
(2)求出角的范围结合三角函数的单调性和最值之间的关系进行求解即可.
解答 解:(Ⅰ)$f(x)=2cosx•sinx+\sqrt{3}cos2x$…(1分)
=$sin2x+\sqrt{3}cos2x$…(2分)
=$2sin(2x+\frac{π}{3})$,…(4分)
因此f(x)的最小正周期为π.…(6分)
(Ⅱ)当$x∈[-\frac{π}{12},\frac{π}{6}]$时,$\frac{π}{6}≤2x+\frac{π}{3}≤\frac{2π}{3}$,…(8分)
当$2x+\frac{π}{3}=\frac{π}{2}$,$sin(2x+\frac{π}{3})$有最大值1.…(10分)
即$x=\frac{π}{12}$时,f(x)的最大值为2.…(13分)
点评 本题主要考查三角函数图象和性质的考查,利用辅助角公式进行化简是解决本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
17.执行如图所示的程序框图,则输出S的值是( )
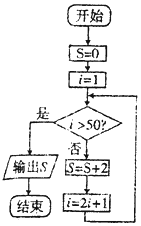

| A. | 10 | B. | 12 | C. | 100 | D. | 102 |
12.已知集合A={x|0<x<2},B={x|x2-1≤0},那么A∪B=( )
| A. | {x|0<x≤1} | B. | {x|-1≤x<2} | C. | {x|-1≤x<0} | D. | {x|1≤x<2} |
19.下列函数中,定义域为R的奇函数是( )
| A. | y=x2+1 | B. | y=tanx | C. | y=2x | D. | y=x+sinx |