题目内容
20.已知关于x的一次函数y=mx+n,设m∈{-1,1,2},n∈{-2,2},则函数y=mx+n是增函数的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
分析 基本事件总数N=3×2=6,函数y=mx+n是增函数需要满足的条件是m>0,从而求出函数y=mx+n是增函数包含的基本事件个数,由此能求出函数y=mx+n是增函数的概率.
解答 解:∵关于x的一次函数y=mx+n,设m∈{-1,1,2},n∈{-2,2},
∴基本事件总数N=3×2=6,
函数y=mx+n是增函数需要满足的条件是m>0,
∴函数y=mx+n是增函数包含的基本事件个数M=2×2=4,
∴函数y=mx+n是增函数的概率p=$\frac{M}{N}=\frac{4}{6}=\frac{2}{3}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为45°,若E是PB的中点,则异面直线DE与PA所成角的余弦值为( )
| A. | $\frac{{3\sqrt{10}}}{20}$ | B. | $\frac{{\sqrt{10}}}{20}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
8.若对于任意的x>0,不等式$\frac{x}{{x}^{2}+3x+1}$≤a恒成立,则实数a的取值范围为( )
| A. | a≥$\frac{1}{5}$ | B. | a>$\frac{1}{5}$ | C. | a<$\frac{1}{5}$ | D. | a≤$\frac{1}{5}$ |
12.已知集合A={x|0<x<2},B={x|x2-1≤0},那么A∪B=( )
| A. | {x|0<x≤1} | B. | {x|-1≤x<2} | C. | {x|-1≤x<0} | D. | {x|1≤x<2} |
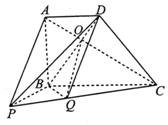 如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.
如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.