题目内容
已知数列f(x)=logkx(k为常数,k>0且k≠1),且数列{f(an)} 首项为a,公差为d的等差数列,且满足不等式|a-4|+|d-2|≤0;
(1)求数列{an}的通项an;
(2)若bn=an•f(an),当k=
时,求数列{bn}的前n项和Sn.
(3)若Cn=anlgan,问是否存在实数k,使得{Cn}中每一项恒小于它后面的项?若存在,求出k的取值范围,若不存在,请说明理由.
(1)求数列{an}的通项an;
(2)若bn=an•f(an),当k=
| 3 |
(3)若Cn=anlgan,问是否存在实数k,使得{Cn}中每一项恒小于它后面的项?若存在,求出k的取值范围,若不存在,请说明理由.
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(1)由已知可得f(an)=2n+2=logkan,an=k2n+2;
(2)当k=
时,bn=(2n+2)•3n+1,利用“乘公比错位相减”求和;
(3)由(1)可知cn=(2n+2)•k2n+2lgk,若使得{cn}中的每一项恒小于它后面的项⇒cn<cn+1⇒(n+1)lgk<(n+2)•k2•lgk对一切n∈N*成立,分①lgk>0②lgk<0讨论求解.
(2)当k=
| 3 |
(3)由(1)可知cn=(2n+2)•k2n+2lgk,若使得{cn}中的每一项恒小于它后面的项⇒cn<cn+1⇒(n+1)lgk<(n+2)•k2•lgk对一切n∈N*成立,分①lgk>0②lgk<0讨论求解.
解答:
解:(1)由题意,a=4,d=2,
∴f(an)=4+(n-1)×2=2n+2,即logkan=2n+2,
∴an=k2n+2;
(2)由(1)知,bn=anf(an)=k2n+2•(2n+2),
当k=
时,bn=(2n+2)•3n+1.
∴Sn=4•32+6•33+…+(2n+2)•3n+1,①
3Sn=4•33+6•34+…+2n•3n+1+(2n+2)•3n+2.②
②-①,得Sn=
;
(3)由(1)知,cn=anlgan=(2n+2)•k2n+2lgk,要使cn<cn+1对一切n∈N*成立,
即(n+1)lgk<(n+2)•k2•lgk对一切n∈N*成立.
①当k>1时,lgk>0,n+1<(n+2)k2对一切n∈N*恒成立;
②当0<k<1时,lgk<0,n+1>(n+2)k2对一切n∈N*恒成立,只需k2<(
)min,
∵
=1-
单调递增,
∴当n=1时,(
)min=
,
∴k2<
,且0<k<1,
∴0<k<
.
综上所述,存在实数k∈(0,
)∪(1,+∞)满足条件.
∴f(an)=4+(n-1)×2=2n+2,即logkan=2n+2,
∴an=k2n+2;
(2)由(1)知,bn=anf(an)=k2n+2•(2n+2),
当k=
| 3 |
∴Sn=4•32+6•33+…+(2n+2)•3n+1,①
3Sn=4•33+6•34+…+2n•3n+1+(2n+2)•3n+2.②
②-①,得Sn=
| (2n+1)•3n+2-9 |
| 2 |
(3)由(1)知,cn=anlgan=(2n+2)•k2n+2lgk,要使cn<cn+1对一切n∈N*成立,
即(n+1)lgk<(n+2)•k2•lgk对一切n∈N*成立.
①当k>1时,lgk>0,n+1<(n+2)k2对一切n∈N*恒成立;
②当0<k<1时,lgk<0,n+1>(n+2)k2对一切n∈N*恒成立,只需k2<(
| n+1 |
| n+2 |
∵
| n+1 |
| n+2 |
| 1 |
| n+2 |
∴当n=1时,(
| n+1 |
| n+2 |
| 2 |
| 3 |
∴k2<
| 2 |
| 3 |
∴0<k<
| ||
| 3 |
综上所述,存在实数k∈(0,
| ||
| 3 |
点评:本题综合考查数列的基本知识、方法和运算能力,渗透了函数的知识,以及分类讨论和化归、转化的思想方法、.错位相减法是数列求和的一种重要方法,学习中要引起重视.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
实数a,b,c满足a>b>c,ac<0,下列不等式一定成立的是( )
| A、c(b-a)<0 |
| B、ab2>cb2 |
| C、c(a-c)>0 |
| D、ab>ac |

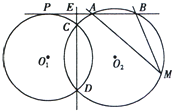 已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.
已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.