题目内容
在空间四边形ABCD中,E、F分别是AD、BC的中点,若AC=BD=a,EF=
a,∠BDC=90°.求证:BD⊥平面ACD.
| ||
| 2 |
考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:作BC的中点G,连接EG,FG,先证明出EG⊥GF,进而证明出BD⊥AC,最后根据线面垂直的判定定理证明出BD⊥平面ACD.
解答:

证明:作DC的中点G,连接EG,FG,
则EG=
AC=
,GF=
BD=
,
∴EG2+GF2=EF2,
∴EF⊥FG,
∵EG∥AC,FG∥BD,
∴BD⊥AC,
∵BD⊥DC,DC?平面ACD,AC?平面ACD,AC∪CD=C,
∴BD⊥平面ACD.

证明:作DC的中点G,连接EG,FG,
则EG=
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
∴EG2+GF2=EF2,
∴EF⊥FG,
∵EG∥AC,FG∥BD,
∴BD⊥AC,
∵BD⊥DC,DC?平面ACD,AC?平面ACD,AC∪CD=C,
∴BD⊥平面ACD.
点评:本题主要考查了线面垂直的判定定理的应用.证明的关键是找到两条相交的与之垂直的直线.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
设i是虚数单位,则满足i2014•z=3-4i的复数z的共轭复数是( )
| A、-3-4i | B、-3+4i |
| C、3-4i | D、3+4i |
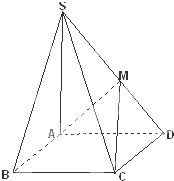 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=AB.
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=AB. 已知函数y=
已知函数y= 如图所示,已知正四棱柱ABCD-A1B1C1D1中,底面边长为2
如图所示,已知正四棱柱ABCD-A1B1C1D1中,底面边长为2