题目内容
从标有1,2,3,…,7的7个小球中取出一个球,记下它上面的数字,放回后再取出一个球,记下它上面的数字,然后把两球上的数字相加,求取出两球上的数字之和大于11或者能被4整除的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:本题先求出有放回的收取两个小球的取法总数,和两球上的数字之和大于11或者能被4整除的取法个数,代入古典概型概率计算公式,可得答案.
解答:
解:从标有1,2,3,…,7的7个小球中取出一个球,记下它上面的数字,放回后再取出一个球,记下它上面的数字,共有7×7=49种不同情况,
其中两球上的数字之和大于11或者能被4整除的事件有:
(1,3),(1,7),(2,2),(2,6),(3,1),(3,5),(4,4),(5,3),
(5,7),(6,2),(6,6),(7,1),(7,5),(6,7),(7,6),(7,7),共16种,
故取出两球上的数字之和大于11或者能被4整除的概率P=
其中两球上的数字之和大于11或者能被4整除的事件有:
(1,3),(1,7),(2,2),(2,6),(3,1),(3,5),(4,4),(5,3),
(5,7),(6,2),(6,6),(7,1),(7,5),(6,7),(7,6),(7,7),共16种,
故取出两球上的数字之和大于11或者能被4整除的概率P=
| 16 |
| 49 |
点评:古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
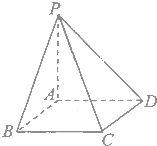 如图,四棱锥P-ABCD的底面ABCD是边长为l的正方形,侧棱PA=1,PB=PD=
如图,四棱锥P-ABCD的底面ABCD是边长为l的正方形,侧棱PA=1,PB=PD=| 2 |
| A、3对 | B、4对 | C、5对 | D、6对 |
二项式(2x-
)5 的展开式中各项系数的和为( )
| 1 | ||
|
| A、1 | B、2 | C、3 | D、4 |