题目内容

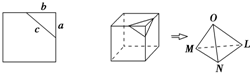在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：c2=a2+b2．设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN，如果用S1，S2，S3表示三个侧面面积，S4表示截面面积，那么你类比得到的结论是
 
．
考点：类比推理
专题：计算题,推理和证明
分析：从平面图形到空间图形，同时模型不变．
解答： 解：建立从平面图形到空间图形的类比，于是作出猜想：
S
2
1
+
S
2
2
+
S
2
3
=
S
2
4
．
故答案为：
S
2
1
+
S
2
2
+
S
2
3
=
S
2
4
．
点评：本题主要考查学生的知识量和知识迁移、类比的基本能力．解题的关键是掌握好类比推理的定义．
练习册系列答案
相关题目
已知函数f（x）满足：f2（x）-2f（x）f（x+1）+2f（x+1）=0（x∈R），
（1）用反证法证明：f（x）不可能为正比例函数；
（2）若f（0）=4，求f（1）、f（2）的值，并用数学归纳法证明：对任意的x∈N*，均有：2＜f（x）＜3．
已知函数f（x）=ax2+bx+c的图象在点（1，f（1））的切线l过点（0，c-1）
（1）求a的值
（2）当b=2c＞0时，函数F（x）=x[f（x）+c2-c]对任意x1，x2∈[-c，c]，不等式|F（x1）-F（x2）|≤
1
3
c恒成立，求c的最大值．
如图所示，A，B为单位圆O上的两点，且点A（1，0），B（
1
2
，
3
2
），点P为弧AB（不包括端点A，B）上的动点，点P（cosθ，sinθ），OP∩AB=C，且
AC
=λ
AB
．
（Ⅰ）求λ（用θ表示）；
（Ⅱ）若
OC
•
AC
=-
1
16
时，求tanθ的值．
函数f（x）=arccosx，x∈[0，1]的最大值为
 
．
观察下列等式；12=12，13+23=32，13+23+33=62，13+23+33+43=102，…根据上述规律，第n个等式为
 
．
设函数f（x）=
x
1-x
（x≠0且x≠1），则f（x）+f（
1
x
）=
 
．
高二年级共有247名同学报名参加数学支教活动，年级组决定从中随机抽取4位代表海中前往黎村小学支教，请你用“随机数表法”确定参加该活动的人员．如果你从000开始对上述同学编号，且选取的首个数字在随机数表的第4行第9列，读数方式为向右，则被选人员的编号为
 
．
随机数表片段（1～5行）
03 47 43 73 86  36 96 47 36 61  46 98 63 71 62  33 26 16 80 45  60 11 14 10 95
97 74 24 67 62  42 81 14 57 20  42 53 32 37 32  27 07 36 07 51  24 51 79 89 73
16 76 62 27 66  56 50 26 71 07  32 90 79 78 53  13 55 38 58 59  88 97 54 14 10
12 56 85 99 26  96 96 68 27 31  05 03 72 93 15  57 12 10 14 21  88 26 49 81 76
55 59 56 35 64  38 54 82 46 22  31 62 43 09 90  06 18 44 32 53  23 83 01 30 30．
若函数y=3+x2ln（
1+x
1-x
），x∈[-
1
2
，
1
2
]的最大值与最小值分别为M，m，则M+m=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网