题目内容
设函数f（x）=
（x≠0且x≠1），则f（x）+f（
）= ．
| x |
| 1-x |
| 1 |
| x |
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（x）+f（
）=
+
=
+
，由此能求出结果．
| 1 |
| x |
| x |
| 1-x |
| ||
1-
|
| x |
| 1-x |
| 1 |
| x-1 |
解答：
解：∵f（x）=
（x≠0且x≠1），
∴f（x）+f（
）=
+
=
+
=
=-1．
故答案为：-1．
| x |
| 1-x |
∴f（x）+f（
| 1 |
| x |
| x |
| 1-x |
| ||
1-
|
=
| x |
| 1-x |
| 1 |
| x-1 |
| x-1 |
| 1-x |
故答案为：-1．
点评：本题考查函数值的求法，是基础题，解题时要认真审题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1=2，E是BC中点．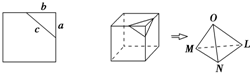
在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：c2=a2+b2．设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN，如果用S1，S2，S3表示三个侧面面积，S4表示截面面积，那么你类比得到的结论是