题目内容
已知函数f(x)=ax2+bx+c的图象在点(1,f(1))的切线l过点(0,c-1)
(1)求a的值
(2)当b=2c>0时,函数F(x)=x[f(x)+c2-c]对任意x1,x2∈[-c,c],不等式|F(x1)-F(x2)|≤
c恒成立,求c的最大值.
(1)求a的值
(2)当b=2c>0时,函数F(x)=x[f(x)+c2-c]对任意x1,x2∈[-c,c],不等式|F(x1)-F(x2)|≤
| 1 |
| 3 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:(1)求出导数,求出切线的斜率,切点坐标,由两点的斜率公式,即可得到a;
(2)化简F(x),求导数,求出在[-c,c]内的极值,以及最值,由条件可知最大值与最小值的差不大于
c,解不等式,即可得到c的最大值.
(2)化简F(x),求导数,求出在[-c,c]内的极值,以及最值,由条件可知最大值与最小值的差不大于
| 1 |
| 3 |
解答:
解:(1)函数f(x)=ax2+bx+c的导数f′(x)=2ax+b,
f′(1)=2a+b,f(1)=a+b+c,
由于切线l过点(0,c-1),则2a+b=
,
∴a=1.
(2)当b=2c>0时,函数F(x)=x[f(x)+c2-c]
=x(x2+2cx+c+c2-c)=x(x+c)2,F′(x)=(x+c)(3x+c),
当-c≤x≤-
时,F′(x)≤0,-
≤x≤c时,F′(x)≥0,
则F(x)在x=-
处取极小值,也为最小值,且为-
c3,
F(c)=4c3,F(-c)=0,则最大值为4c3,
由于对任意x1,x2∈[-c,c],不等式|F(x1)-F(x2)|≤
c恒成立,
即有
c≥4c3-(-
c3),
由于c>0,则c≤
,
故c的最大值为
.
f′(1)=2a+b,f(1)=a+b+c,
由于切线l过点(0,c-1),则2a+b=
| a+b+c-(c-1) |
| 1 |
∴a=1.
(2)当b=2c>0时,函数F(x)=x[f(x)+c2-c]
=x(x2+2cx+c+c2-c)=x(x+c)2,F′(x)=(x+c)(3x+c),
当-c≤x≤-
| c |
| 3 |
| c |
| 3 |
则F(x)在x=-
| c |
| 3 |
| 4 |
| 27 |
F(c)=4c3,F(-c)=0,则最大值为4c3,
由于对任意x1,x2∈[-c,c],不等式|F(x1)-F(x2)|≤
| 1 |
| 3 |
即有
| 1 |
| 3 |
| 4 |
| 27 |
由于c>0,则c≤
3
| ||
| 28 |
故c的最大值为
3
| ||
| 28 |
点评:本题考查导数的综合应用:求切线,求单调区间和极值,以及最值,考查不等式的恒成立问题转化为求函数的最值问题,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.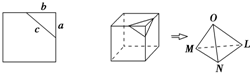 在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是
在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是