题目内容
 如图所示,A,B为单位圆O上的两点,且点A(1,0),B(
如图所示,A,B为单位圆O上的两点,且点A(1,0),B(| 1 |
| 2 |
| ||
| 2 |
| AC |
| AB |
(Ⅰ)求λ(用θ表示);
(Ⅱ)若
| OC |
| AC |
| 1 |
| 16 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(Ⅰ)由条件利用两个向量的数量积公式,两个向量坐标形式的运算法则可得
=(1-
,
λ),根据
∥
,可得
=
,由此λ 的值.
(Ⅱ)由
•
=
-
=-
,求得λ=
,可得
=
,由此求得tanθ 的值.
| OC |
| λ |
| 2 |
| ||
| 2 |
| OP |
| OC |
1-
| ||
| cosθ |
| ||||
| sinθ |
(Ⅱ)由
| OC |
| AC |
| λ2 |
| 2 |
| λ |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
| sinθ | ||
sin(θ+
|
| 1 |
| 4 |
解答:
解:(Ⅰ)由题意可得
=
-
=λ•
=λ(-
,
),∴
=(1-
,
λ).
又
=(cosθ,sinθ),
∥
,∴
=
,∴λ=
.
(Ⅱ)∵
•
=(1-
,
λ)•(-
,
λ)=
-
=-
,求得λ=
,
∴
=
,求得tanθ=
.
| AC |
| OC |
| OA |
| AB |
| 1 |
| 2 |
| ||
| 2 |
| OC |
| λ |
| 2 |
| ||
| 2 |
又
| OP |
| OP |
| OC |
1-
| ||
| cosθ |
| ||||
| sinθ |
| sinθ | ||
sin(θ+
|
(Ⅱ)∵
| OC |
| AC |
| λ |
| 2 |
| ||
| 2 |
| λ |
| 2 |
| ||
| 2 |
| λ2 |
| 2 |
| λ |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
∴
| sinθ | ||
sin(θ+
|
| 1 |
| 4 |
| ||
| 7 |
点评:本题主要考查两个向量的数量积公式,两个向量坐标形式的运算,两个向量共线的性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
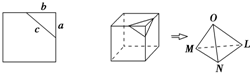 在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是
在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是